Scalable Unsupervised Alignment

Learning to align general metric and non-metric structures through amortized Gromov-Wasserstein optimization

ICML AI4Science Workshop 2024

TL;DR: We transform the computationally intractable Gromov-Wasserstein problem into a scalable, inductive solution by learning embeddings that map domains into a common space where alignment reduces to a single optimal transport problem. This enables handling 45,000+ samples where standard solvers fail beyond 25,000, with extensions to non-metric structures through rank-based matching.

Overview

Aligning data from different domains is fundamental in machine learning, from single-cell multiomics to neural latent space alignment. This work introduces a learnable Gromov-Wasserstein framework that transforms the computationally intractable quadratic assignment problem into a scalable, inductive solution.

Rather than solving Gromov-Wasserstein (GW) problems directly through iterative optimization, we learn embeddings that map both domains into a common space where a single optimal transport problem produces the alignment. This amortized approach enables:

Inductive generalization: Train on small samples, apply to arbitrarily large test sets
Superior scalability: Handle 45,000+ samples where standard solvers fail beyond 25,000
Flexible extensions: Support non-metric structures through rank-based matching

Comparison of approaches: Entropic GW (left) iteratively solves multiple optimal transport problems. Our method (right) learns embeddings f and g that directly produce the alignment via a single OT problem, amortizing the computational cost.

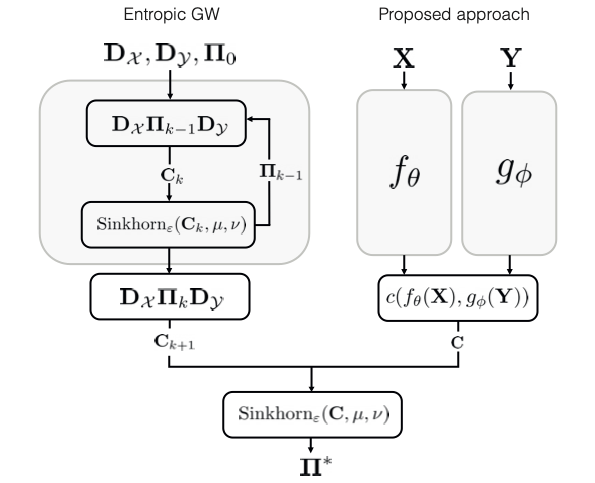
Method: Learning Alignment Through Bilevel Optimization

From Quadratic to Linear Assignment

The Gromov-Wasserstein problem seeks to align metric spaces by minimizing distance disagreement:

\[d^2_{\text{GW}} = \min_{\mathbf{\Pi} \in U(\mu, \nu)} \| \mathbf{D}_\mathcal{X} - \mathbf{\Pi} \mathbf{D}_\mathcal{Y} \mathbf{\Pi}^\T \|_\mathrm{F}^2\]

This is a quadratic assignment problem (NP-hard). Instead of solving it directly, we pose a bilevel optimization:

\[\begin{aligned} \Vec{\Pi}^* =& \argmin_{\theta, \phi} \, \left\| \mathbf{D}_\mathcal{X} - \Vec{\Pi}(\theta, \phi) \mathbf{D}_\mathcal{Y} \Vec{\Pi}^\T(\theta, \phi) \right\|_{\mathrm{F}}^2 \\ & \,\, \text{s.t.} \,\, \Vec{\Pi}(\theta, \phi) = \argmin_{\Vec{\Pi} \in U(\mu, \nu)} \langle \mathbf{\Pi}, {c}(f_\theta(\mathbf{X}), g_\phi(\mathbf{Y}))\rangle \end{aligned}\]

Here, $f_\theta$ and $g_\phi$ are neural networks that embed samples from $\mathcal{X}$ and $\mathcal{Y}$ into a common space. The inner problem is a linear optimal transport problem, efficiently solvable via Sinkhorn algorithm.

Key Insight: Amortization

By learning the embeddings, we amortize the iterative GW computation. At inference:

Embed new samples through learned $f_\theta$ and $g_\phi$
Solve a single entropy-regularized OT problem
No need to recompute geodesic distances or iterate through GW loops

This is implemented using implicit differentiation to backpropagate gradients through the OT solver, enabling end-to-end learning.

Inductive alignment on Swiss roll manifolds. The learned embeddings generalize to new samples, correctly recovering correspondences between isometric manifolds with different embeddings in ambient space.

Extensions: Making It Practical

1. Rank-Based Matching for Non-Metric Structures

Standard GW requires metric spaces. For general dissimilarities (e.g., different biological modalities with incompatible scales), we match ranks instead of distances:

\[\min_{\theta, \phi} \left\| \mathcal{R}_\delta\left(\mathbf{D}_\mathcal{X}\right) - \mathcal{R}_\delta\left(\mathbf{\Pi}(\theta, \phi) \mathbf{D}_\mathcal{Y} \mathbf{\Pi}^\T(\theta, \phi) \right) \right\|_{\mathrm{F}}^2\]

where $\mathcal{R}_\delta$ is a differentiable soft-ranking operator. This makes the method:

Scale-invariant: Handles point clouds differing by arbitrary scale factors
Monotone-invariant: Robust to monotone transformations of dissimilarities
Broadly applicable: Works with non-metric single-cell multiomics data

Rank-based matching on Swiss roll manifolds with simulated annealing. This formulation is robust to scale differences and monotone transformations, making it ideal for aligning non-metric structures like biological data from different modalities.

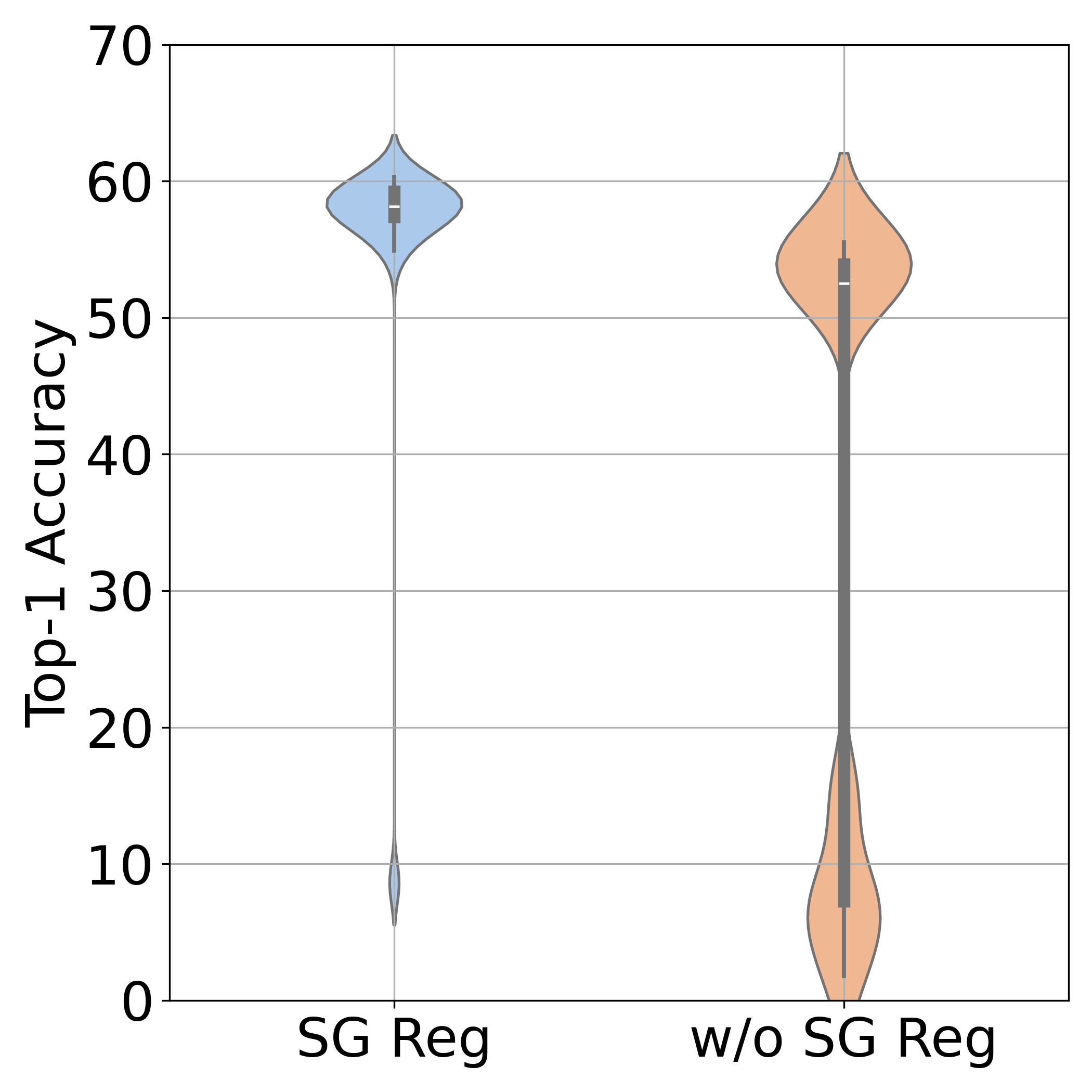
2. Spectral Geometric Regularization

We regularize the learned cost to be smooth on the product manifold:

\[\mathcal{E}_{\text{sm}} = \mathrm{trace}\left( \mathbf{C}^\T \mathbf{L}_{\mathcal{X}} \mathbf{C} + \mathbf{C} \mathbf{L}_\mathcal{Y} \mathbf{C}^\T \right)\]

where $\mathbf{L}\mathcal{X}$ and $\mathbf{L}\mathcal{Y}$ are graph Laplacians. This encodes the intuition: similar samples in one domain should have similar costs relative to the other domain.

Effect of spectral geometric regularization: +20% accuracy improvement and dramatic variance reduction across random seeds.

3. Simulated Annealing of Entropic Regularization

To avoid bad local minima, we gradually decrease the entropy regularization $\epsilon$ during training:

High $\epsilon$ initially: Soft assignments provide global structure
Low $\epsilon$ at end: Sharp assignments for precise alignment
Coarse-to-fine refinement: Similar to multi-scale kernel matching in shape correspondence

Simulated annealing eliminates initialization sensitivity, reducing variance across 20 random seeds to near-zero and breaking symmetry-induced local minima.

Experiments

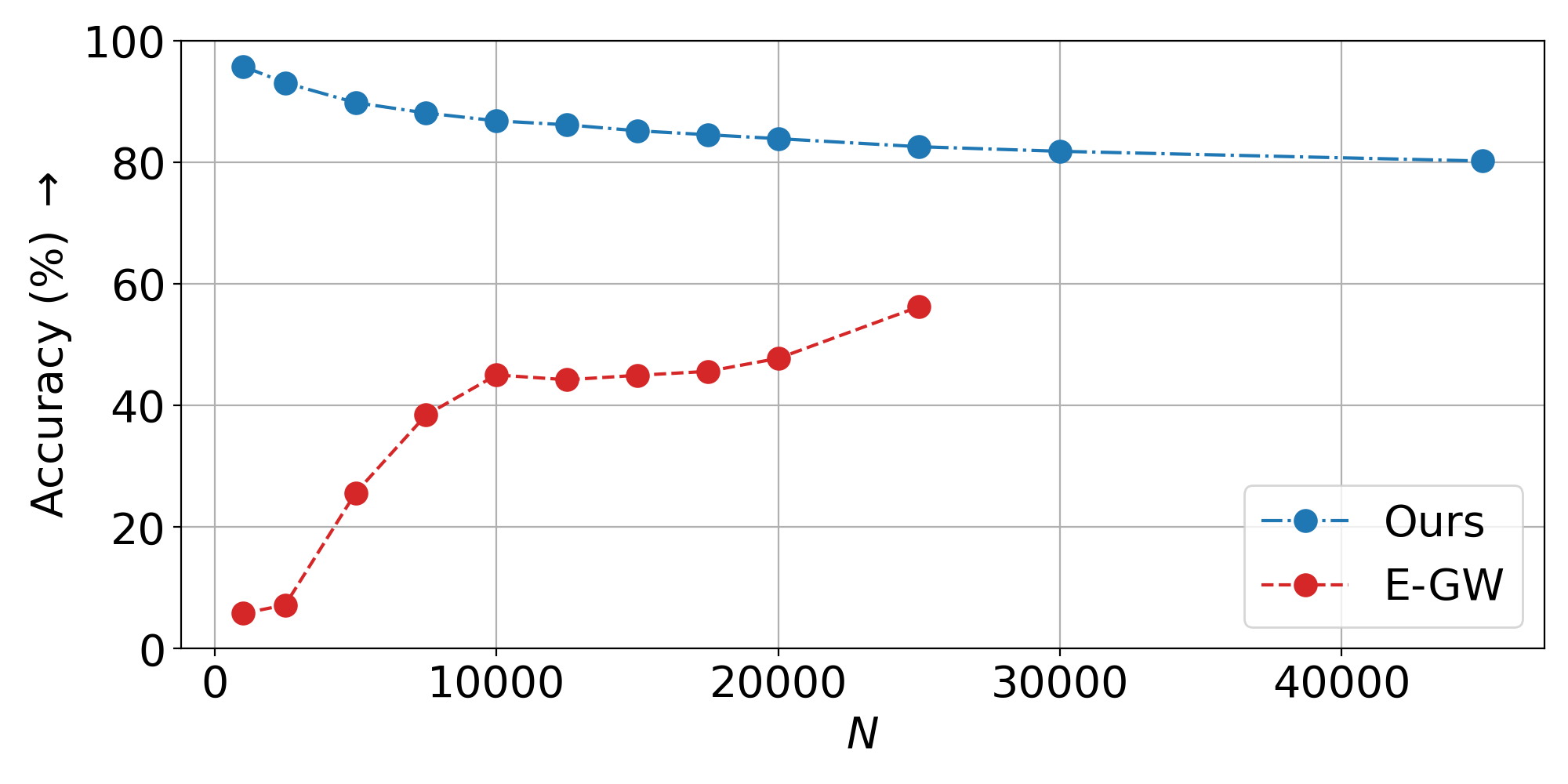
Scalability and Inductivity

We evaluate on CIFAR100 vision transformer embeddings under isometric (orthogonal) and non-isometric (rescaling) transformations.

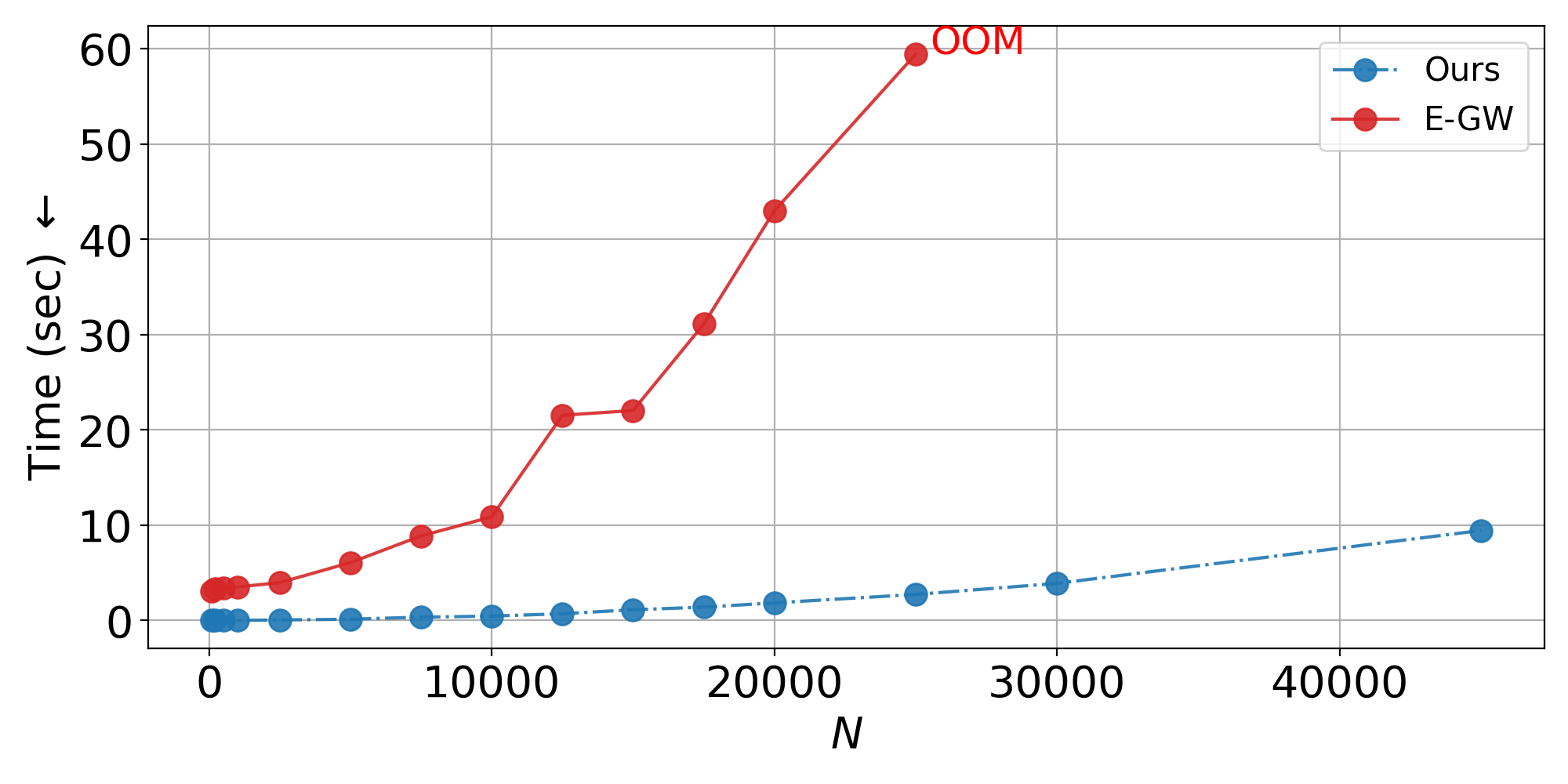
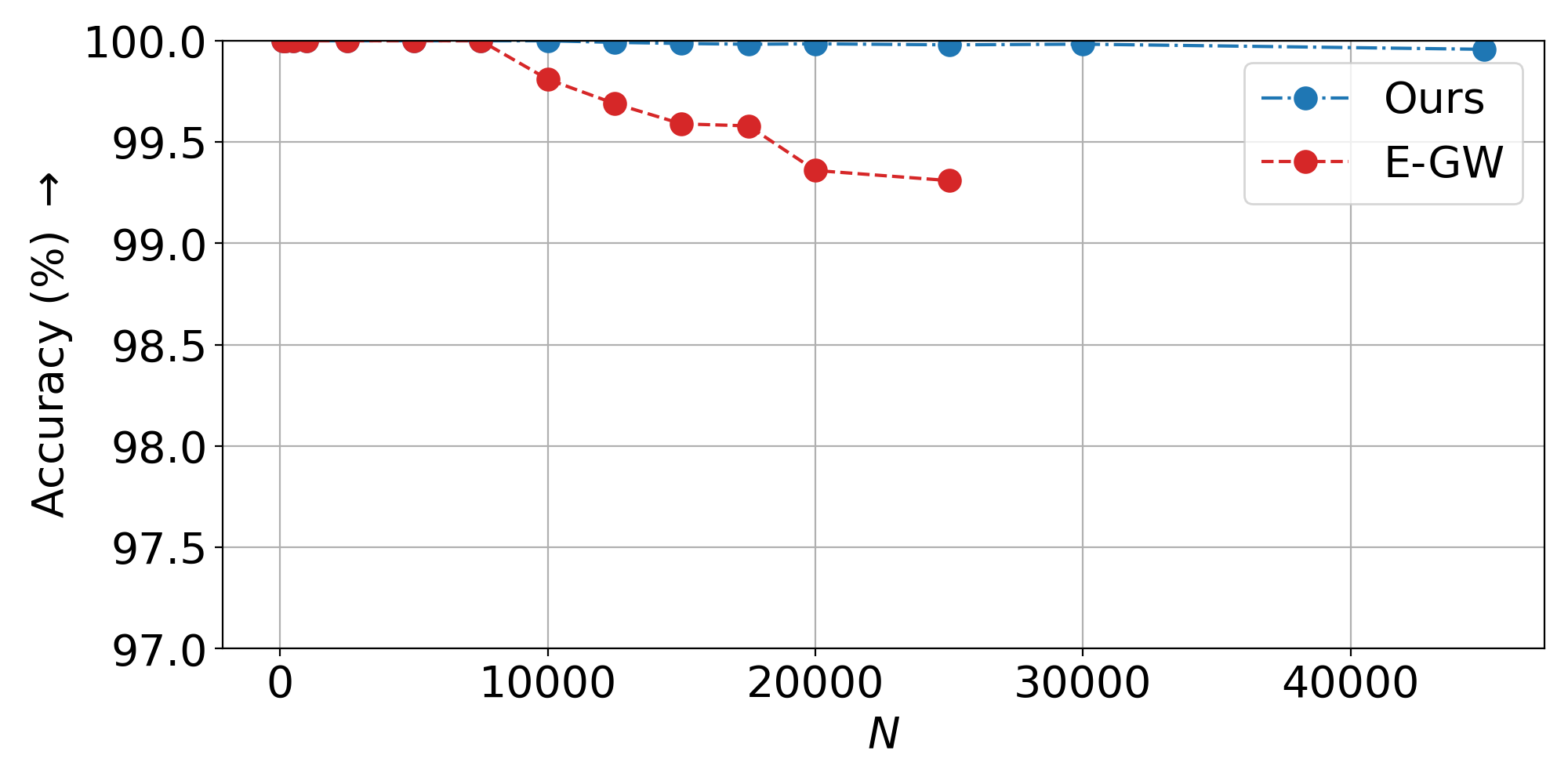
Isometric Setting: Training on 200 samples for 12 seconds, we evaluate inductively on up to 45,000 samples.

Isometric transformation results. Left: Runtime vs. sample size. Right: Accuracy vs. sample size. Our method scales linearly to 45K samples while entropic GW fails beyond 25K. Both achieve perfect accuracy when they can run.

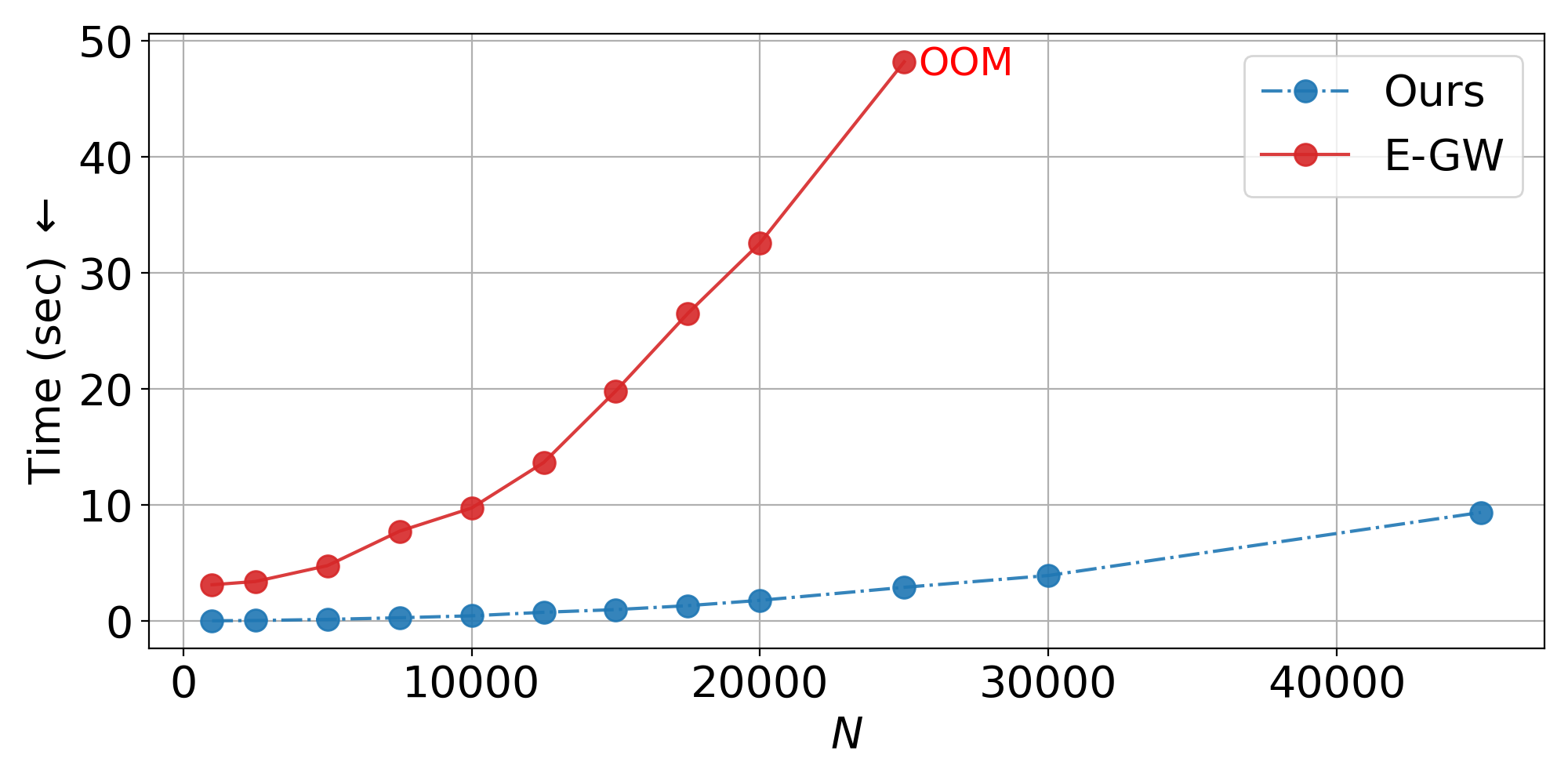
Non-Isometric Setting: ViT embeddings from rescaled images (384x384 vs 256x256), trained on 1,000 samples.

Non-isometric transformation results. Our solver maintains high accuracy and scalability even when spaces are distorted (rescaled images). Entropic GW produces inferior results in this more challenging setting.

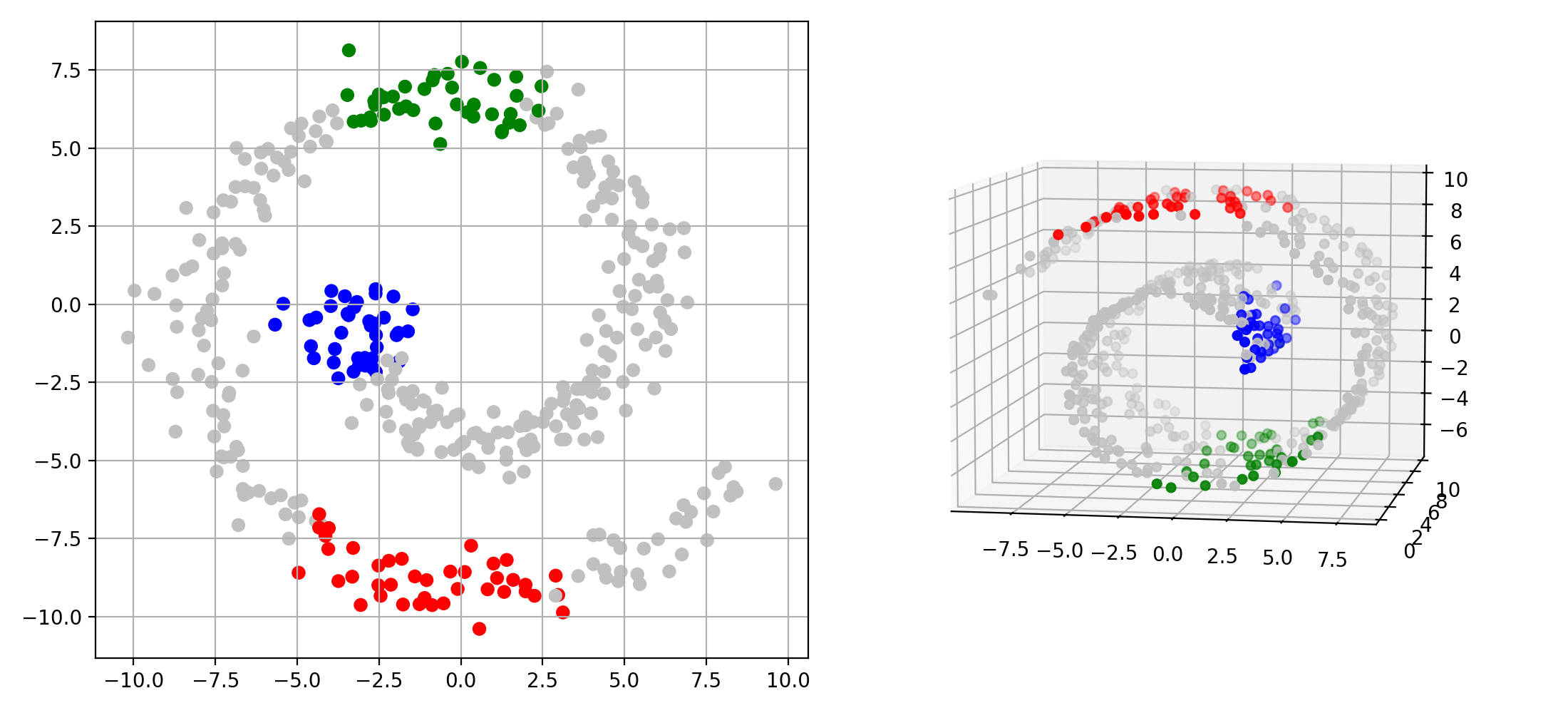
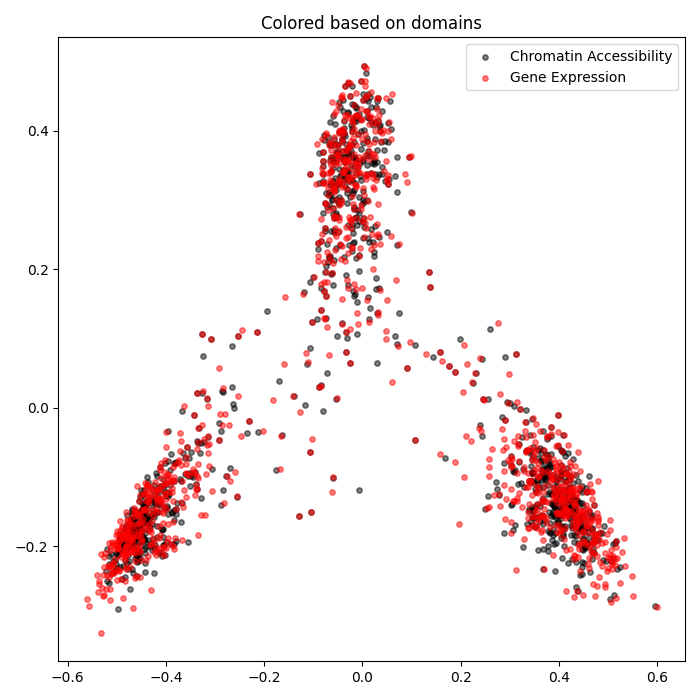
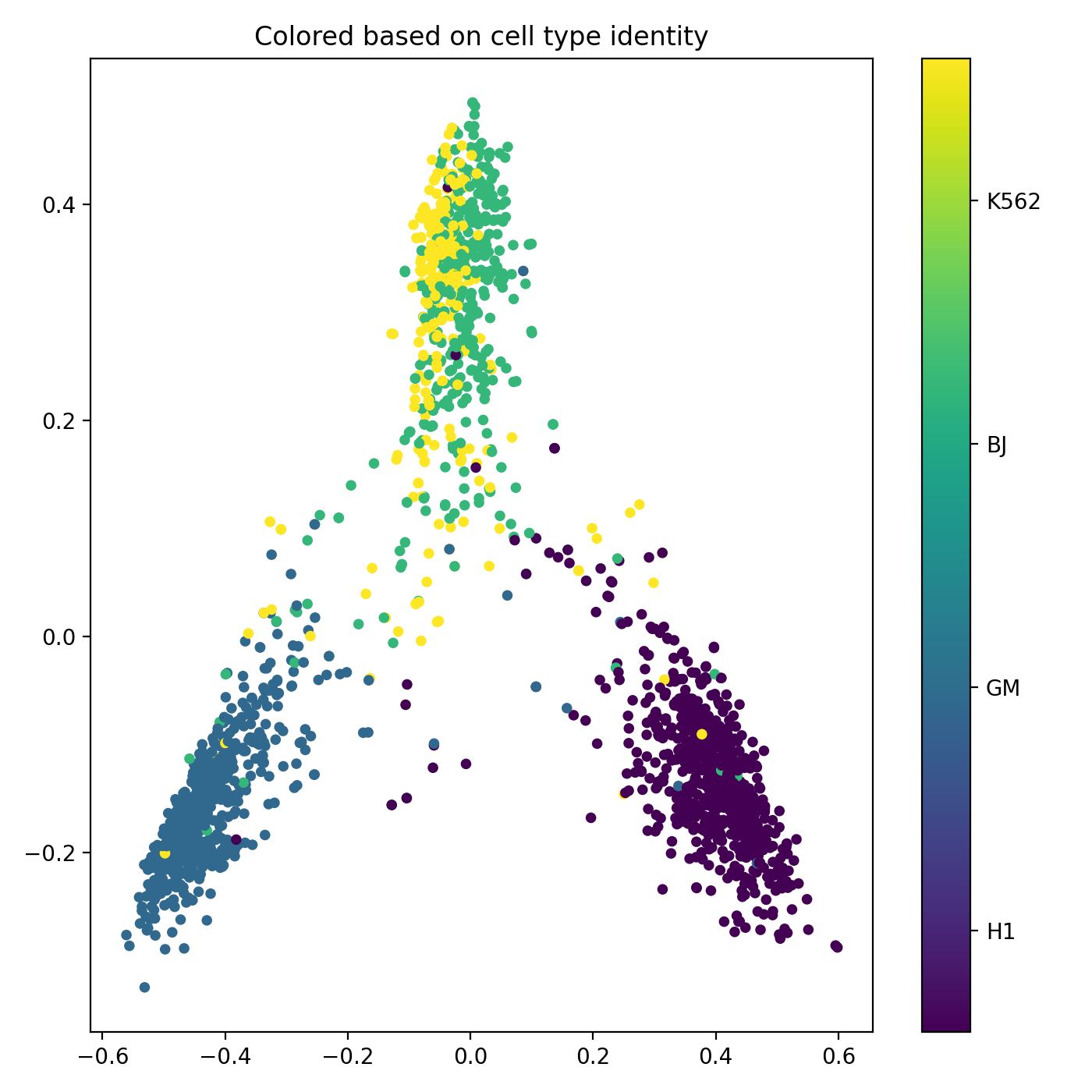
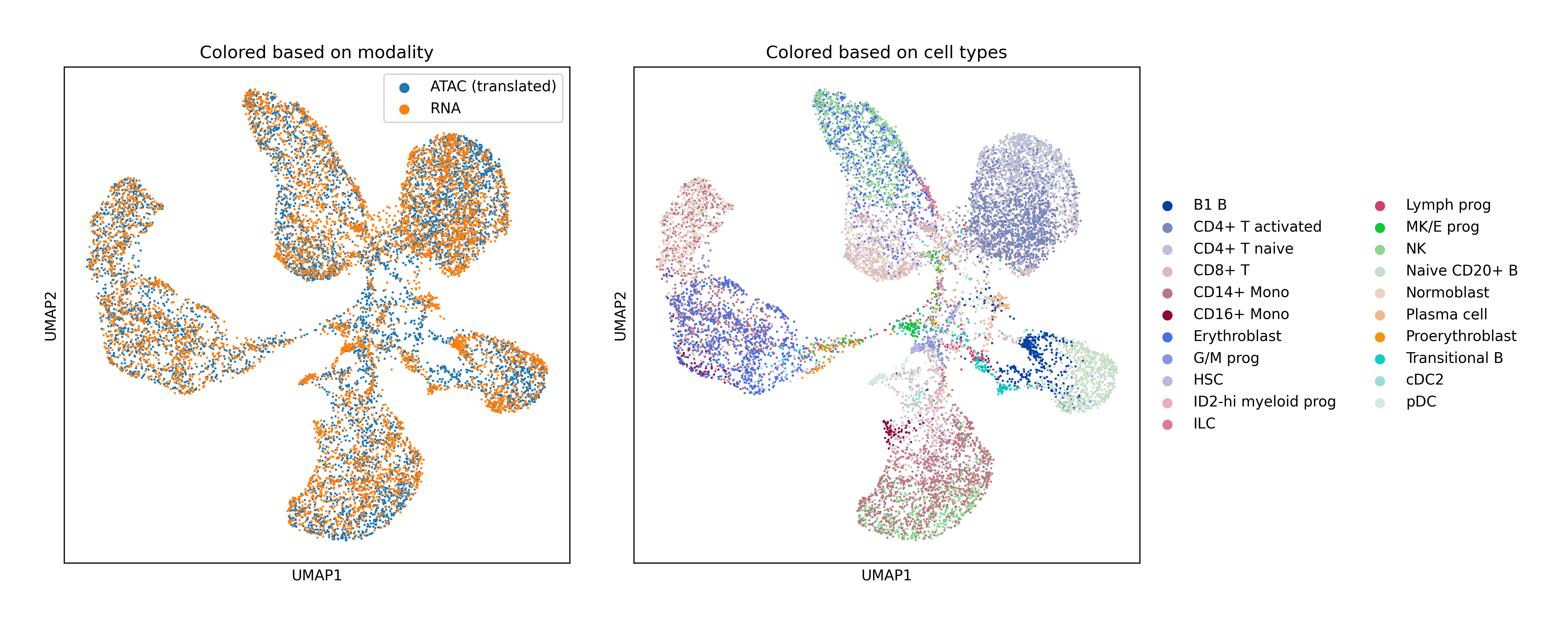
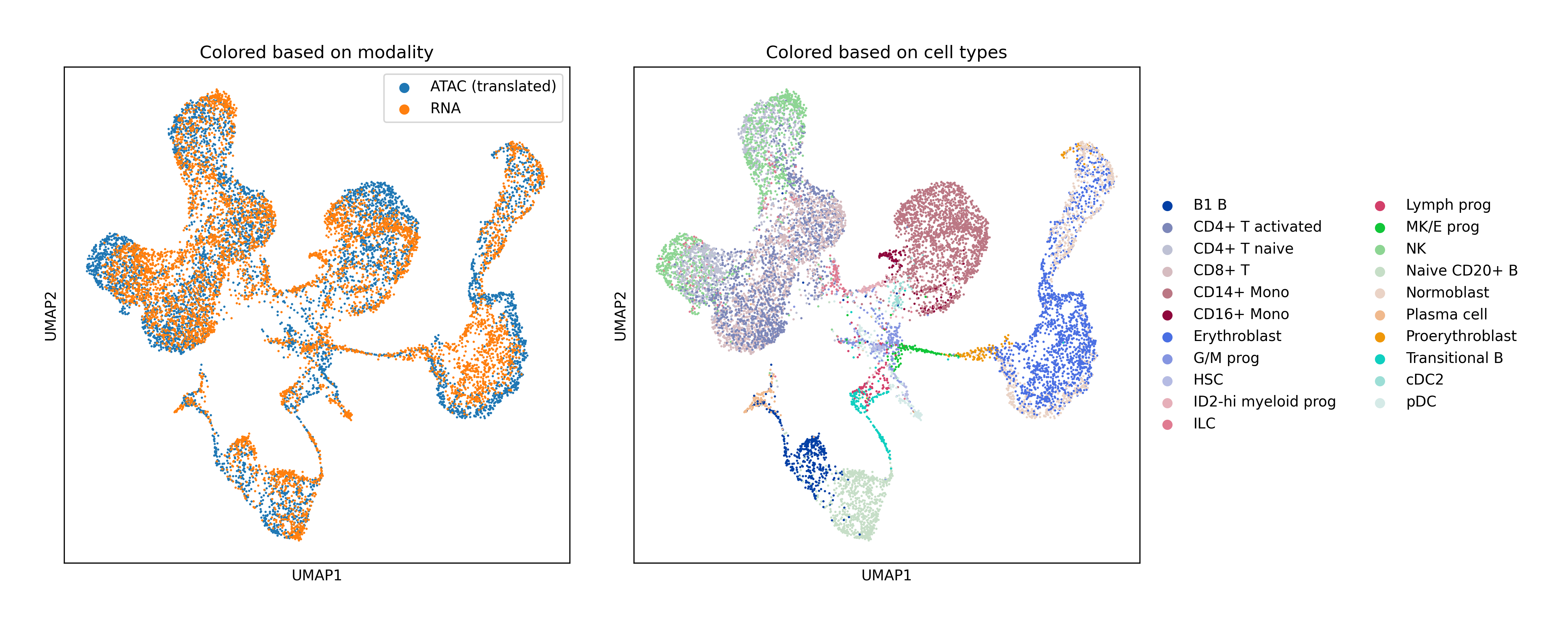
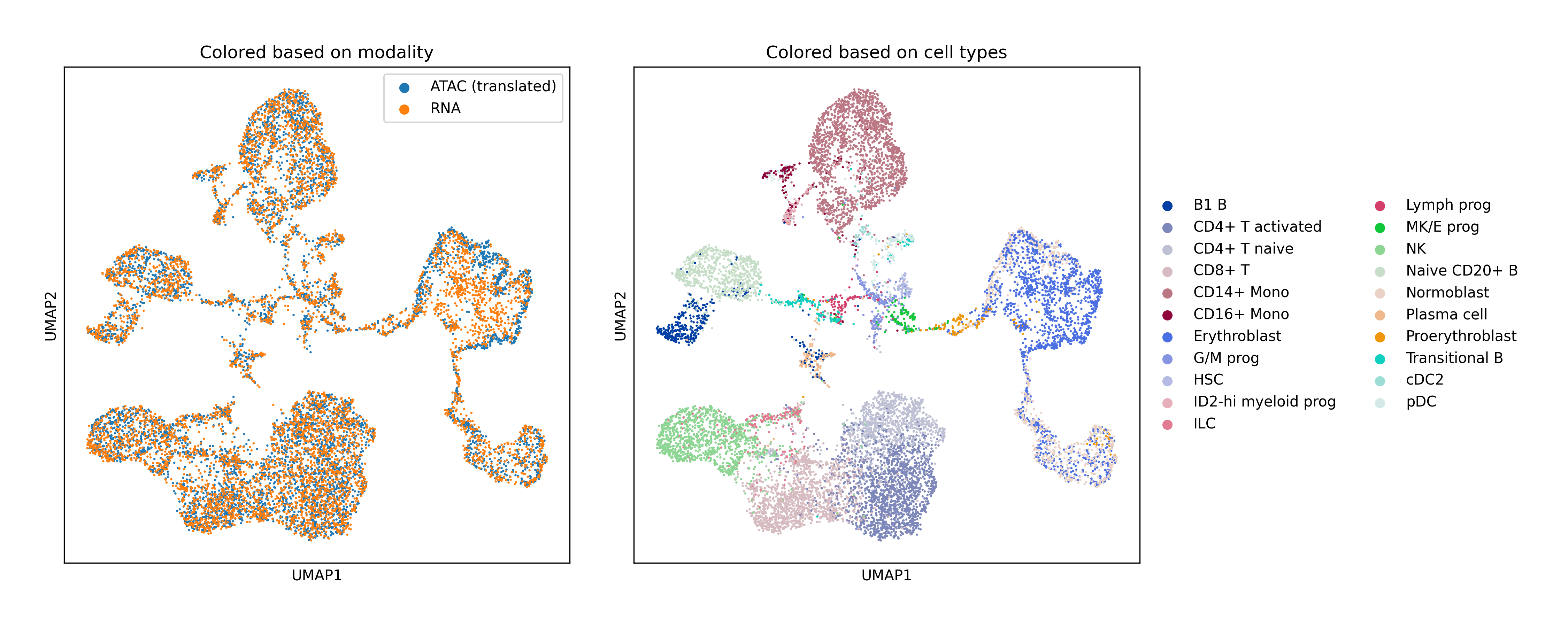
Single-Cell Multiomics Alignment

scSNARE-seq: Aligning RNA (gene expression) and ATAC (chromatin accessibility) from 1,047 cells across 4 cell lines.

scSNARE-seq results. Left: Joint embedding colored by modality (ATAC: black, RNA: red). Right: Colored by cell type. Good mixing of modalities while preserving biological structure.

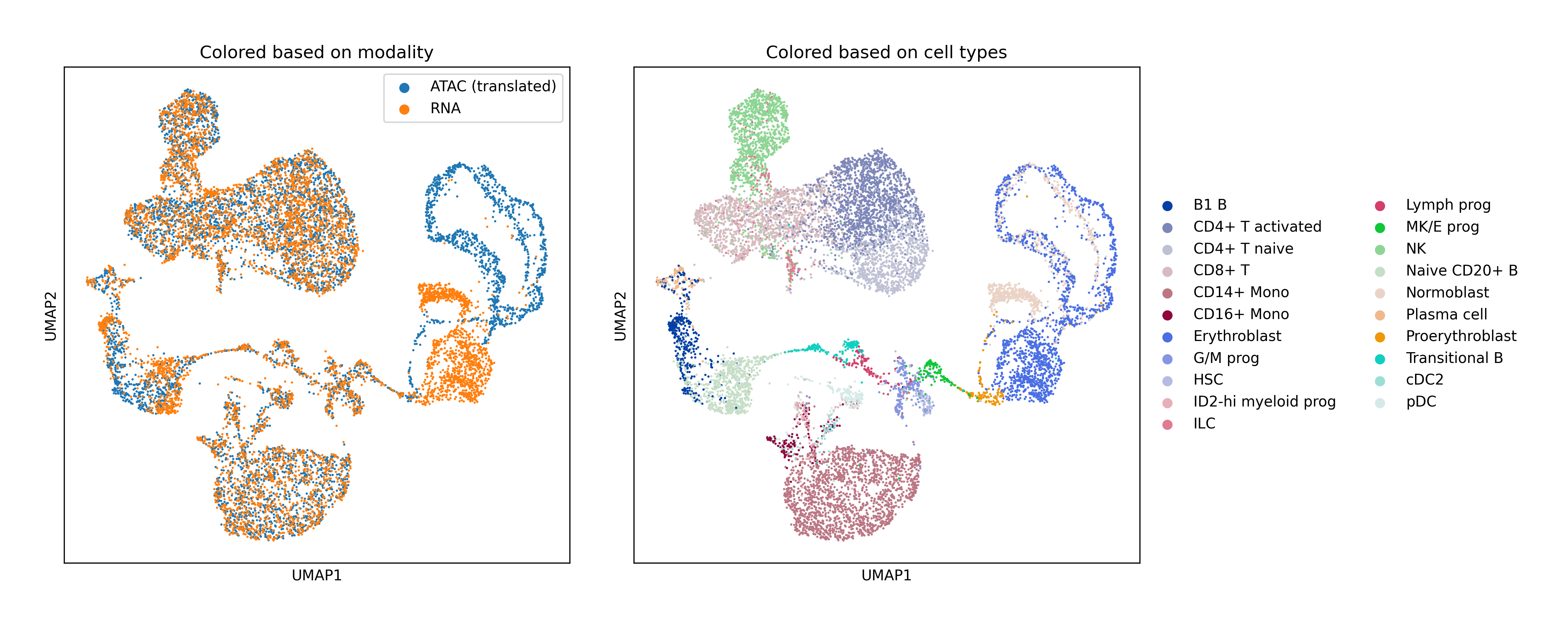
Human Bone Marrow: Large-scale alignment of RNA-seq and ATAC-seq with extensive hyperparameter search for fair baseline comparison.

UMAP visualization of aligned bone marrow cells (our rank-based method). Left: Colored by modality. Right: Colored by cell type. The rank-based solver successfully integrates disparate molecular measurements while preserving biological identity.

Comparison of alignment methods on bone marrow data. Left: Entropic GW with Euclidean distances. Middle: Entropic GW with geodesic distances. Right: Our method with distance matching (before rank-based formulation). All methods show modality mixing, but quantitative metrics reveal our rank-based approach (figure above) achieves superior alignment quality.

Quantitative results on bone marrow data. FOSCTTM (Fraction of Samples Closer Than True Match) for both projection directions. Our rank-based solver (blue) achieves significantly better alignment than entropic GW with Euclidean (orange) or geodesic (green) distances.

Key Findings

Inductive scalability: Train on hundreds of samples, generalize to tens of thousands—nearly 2x beyond the memory limit of standard entropic GW solvers.
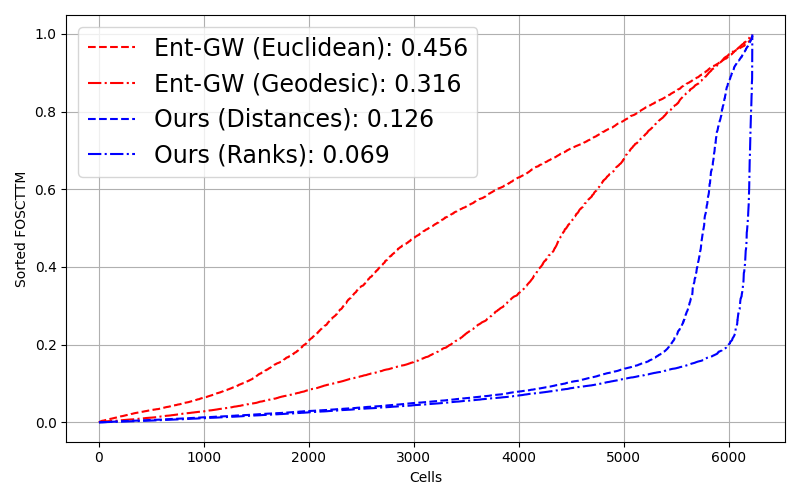
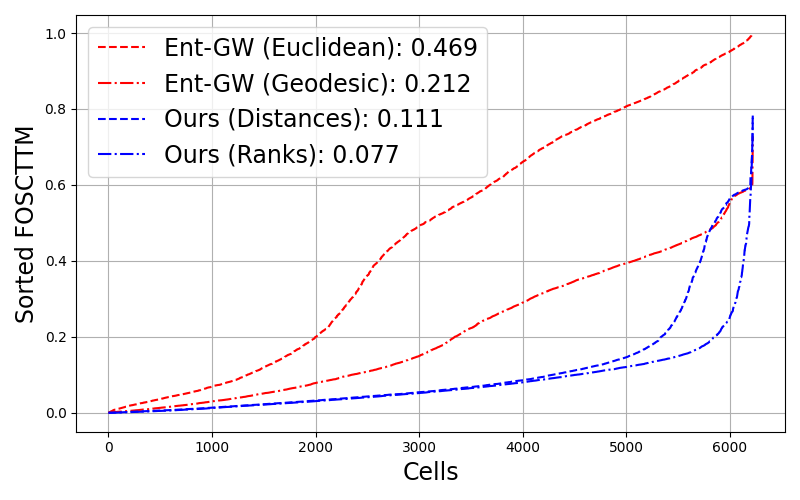
Rank-based matching wins: For real biological data with incompatible scales across modalities, matching distance ranks outperforms matching absolute distances. This extension enables alignment of truly non-metric structures.
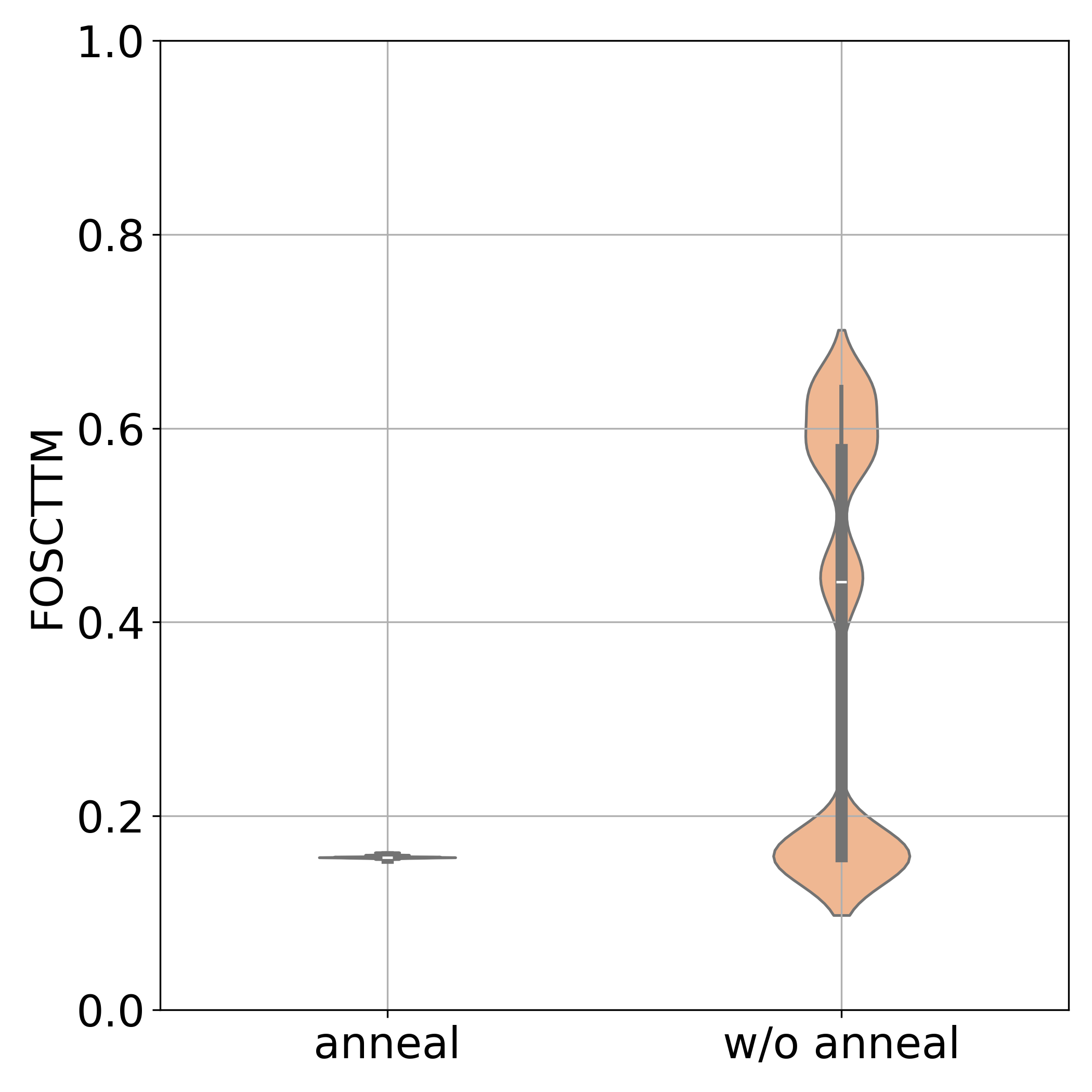
Stabilization matters: Spectral regularization (+20% accuracy) and simulated annealing (near-zero variance) are crucial for reliable performance. These techniques break symmetries and avoid poor local minima.
Amortization pays off: By learning embeddings once, inference requires only a single efficient OT solve—no geodesic computation, no GW iterations. Training time is amortized across all future alignment tasks.
State-of-the-art on multiomics: Outperforms entropic GW and SCOT on single-cell RNA-ATAC alignment tasks, especially at larger scales. The rank-based formulation is particularly effective for disparate biological modalities.

Visual Summary

The method achieves superior alignment quality through three key innovations visible in the results:

Scalability plots: Linear runtime scaling to 45K+ samples vs. memory failure of baselines at 25K
Regularization effects: Dramatic variance reduction and accuracy gains from spectral smoothness and annealing
Biological validation: Clean modality mixing with preserved cell type structure in UMAP visualizations
Quantitative superiority: Significantly lower FOSCTTM scores compared to all baselines on bone marrow data

Citation

@inproceedings{vedula2024scalable,
  title     = {Scalable unsupervised alignment of general metric and non-metric structures},
  author    = {Vedula, Sanketh and Maiorca, Valentino and Basile, Lorenzo and
               Locatello, Francesco and Bronstein, Alex},
  booktitle = {ICML AI4Science Workshop},
  year      = {2024},
  url       = {https://arxiv.org/abs/2406.13507}
}

Authors

Sanketh Vedula¹’² · Valentino Maiorca²’³ · Lorenzo Basile²’⁴ · Francesco Locatello² · Alex Bronstein¹’²

¹Technion, Israel · ²Institute of Science and Technology Austria · ³Sapienza University of Rome, Italy · ⁴University of Trieste, Italy

Applications: This method enables alignment of diverse data types—from single-cell genomics to neural latent spaces—without paired supervision. The rank-based formulation opens doors to truly non-metric alignment problems previously inaccessible to standard Gromov-Wasserstein solvers.