Relative Representations Enable Zero-Shot Latent Space Communication
A novel approach to make neural network latent spaces invariant to training stochasticity, enabling zero-shot model stitching and latent space communication
ICLR 2023
Overview
Neural networks embed high-dimensional data into latent representations, but these representations are affected by random factors like weight initialization, data shuffling, and training hyperparameters. Even when trained on the same data and task, different training runs produce intrinsically similar but extrinsically different latent spaces—they preserve distances between embeddings but differ in absolute coordinates.
We observe empirically that the angles between encodings within distinct latent spaces remain stable across different trainings. Building on this insight, we propose relative representations: representing each data point by its similarity to a fixed set of anchor samples, rather than as an independent vector in \(\mathbb{R}^d\).
This simple change makes latent spaces invariant to isometries and rescalings by construction, enabling:
- Zero-shot model stitching: connecting encoders and decoders from different trainings without any additional training
- Latent space comparison: quantitatively comparing representations across diverse settings
- Cross-modal transfer: stitching models trained on different languages, architectures, or even datasets
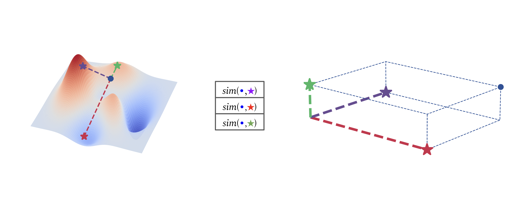
Method: Relative Representations
The Problem
Standard neural networks learn an embedding function \(E_\theta : \mathcal{X} \rightarrow \mathbb{R}^d\) mapping data to absolute representations. While the learned latent space should ideally depend only on the data, task, and architecture, in practice it’s also affected by stochastic factors \(\phi\) (initialization, data shuffling, hyperparameters).
These factors induce transformations \(T\) over the latent space: \(\phi \rightarrow \phi' \Rightarrow E_\theta(x^{(i)}) \rightarrow T E_\theta(x^{(i)})\).
Key Observation: The transformation \(T\) preserves angles between embeddings, i.e., \(\angle(e_{x^{(i)}}, e_{x^{(j)}}) = \angle(Te_{x^{(i)}}, Te_{x^{(j)}})\) for all data pairs.
Relative Representation Construction
We select a subset \(\mathcal{A}\) of anchor samples from the training data. For each data point \(x^{(i)}\), we define its relative representation as:
\[r_{x^{(i)}} = \left(\text{sim}(e_{x^{(i)}}, e_{a^{(1)}}), \text{sim}(e_{x^{(i)}}, e_{a^{(2)}}), \ldots, \text{sim}(e_{x^{(i)}}, e_{a^{(|\mathcal{A}|)}})\right)\]where \(\text{sim} : \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}\) is a similarity function.
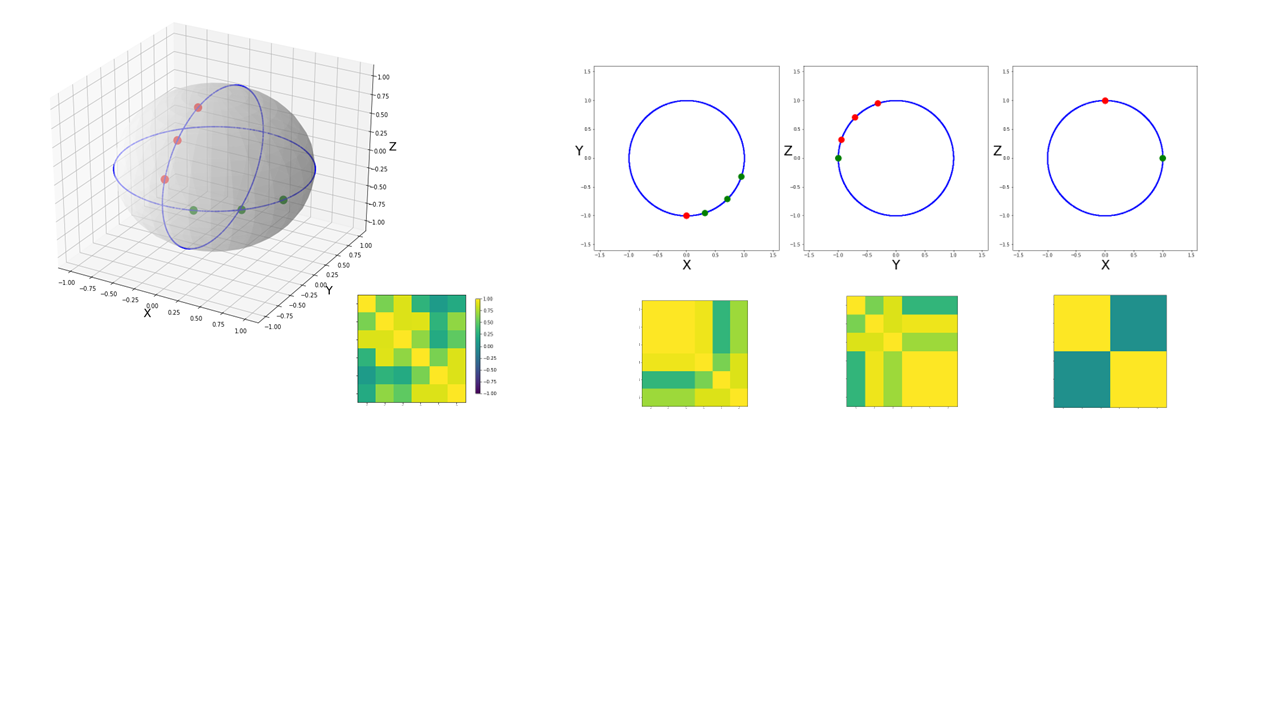
Achieving Invariance with Cosine Similarity
We use cosine similarity as the similarity function:
\[S_C(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{||\mathbf{a}|| \, ||\mathbf{b}||} = \cos \theta\]Cosine similarity is invariant to rotations, reflections, and rescaling. Combined with the normalization techniques commonly used in neural networks (which center latent spaces), this guarantees that relative representations remain unchanged under angle-preserving transformations:
\[[S_C(e_{x^{(i)}}, e_{a^{(1)}}), \ldots, S_C(e_{x^{(i)}}, e_{a^{(|\mathcal{A}|)}})] = [S_C(\tilde{e}_{x^{(i)}}, \tilde{e}_{a^{(1)}}), \ldots, S_C(\tilde{e}_{x^{(i)}}, \tilde{e}_{a^{(|\mathcal{A}|)}})]\]where \(\tilde{e}_{x^{(i)}} = T E(x^{(i)})\) for any angle-preserving transformation \(T\).
Anchor Selection Strategies
Anchors can be chosen in multiple ways:
- Random sampling: Uniform selection from training data
- Parallel anchors: When data comes from different domains with known correspondences (e.g., translated text)
- OOD anchors: Out-of-domain samples for domain adaptation tasks
The number and diversity of anchors affects representation expressivity—more anchors generally improve performance when using frozen encoders.
Latent Space Communication
Word Embeddings Alignment
We compared FastText and Word2Vec embeddings on ~20K English words using 300 randomly selected parallel anchors. The results demonstrate that relative representations effectively align different embedding spaces:
Similarity Metrics (K=10, averaged over 20K words):
- Jaccard similarity: 34-39% exact neighborhood matches (vs. 0% for absolute)
- Mean Reciprocal Rank: 0.94-0.98 (vs. 0.00 for absolute)
- Cosine similarity: 0.86 (vs. 0.01 for absolute)
The absolute representations from FastText and Word2Vec are completely incompatible, while relative representations achieve high similarity despite being trained on different data and architectures.
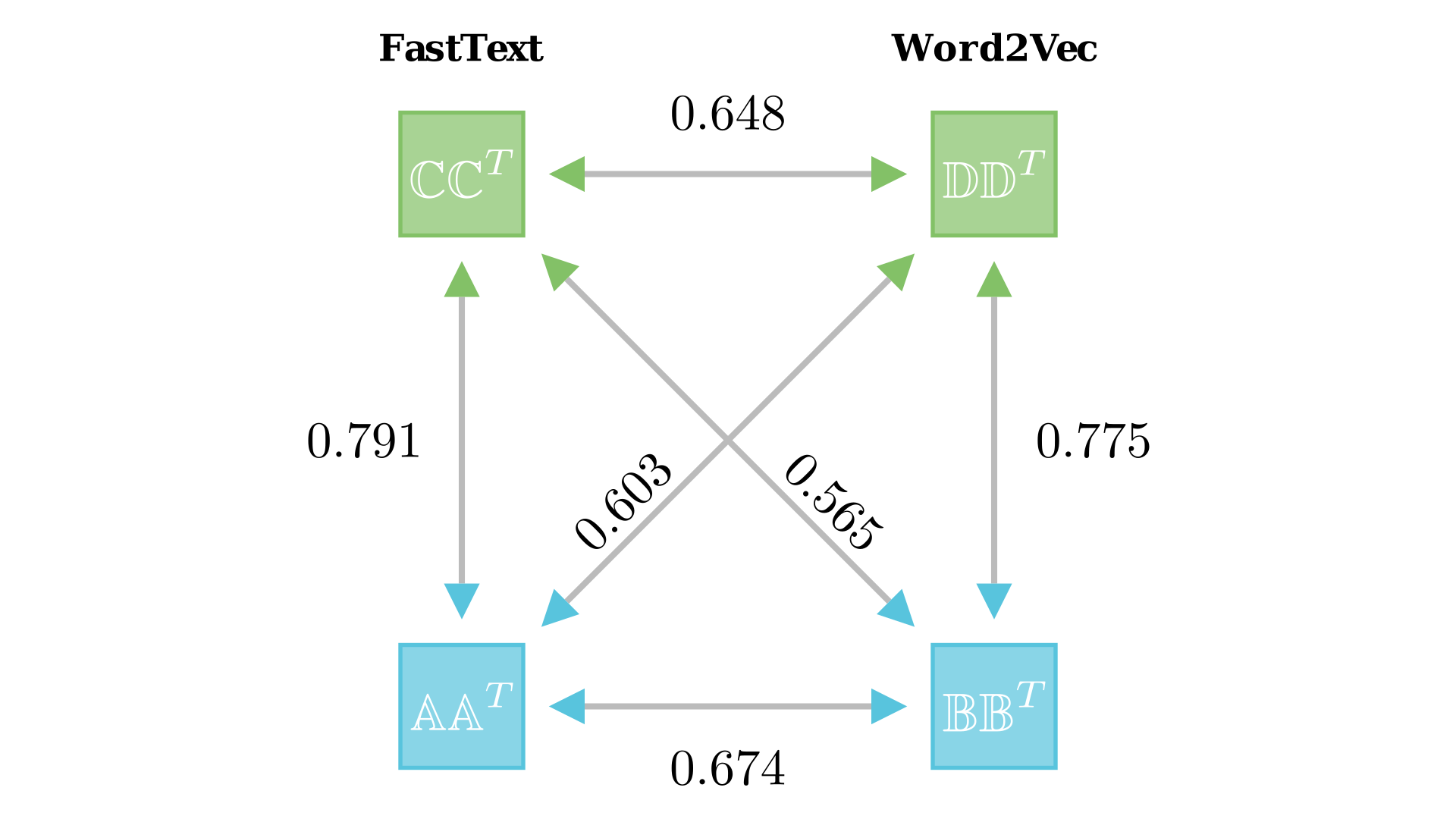
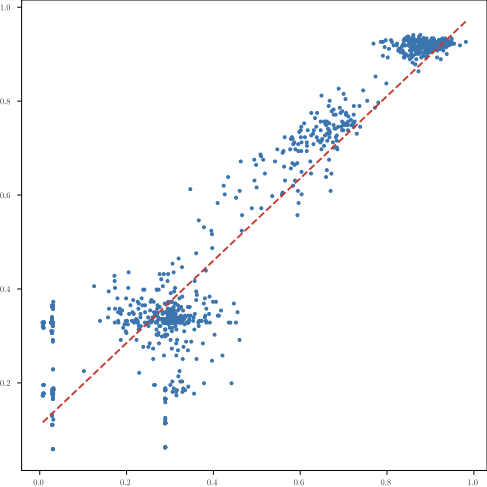
Latent Distance as Performance Proxy
On the Cora graph classification task, we trained ~2000 models with varying hyperparameters (layers, dropout, optimizers, activations, learning rates). We measured:
- Classification accuracy on a validation set
- Similarity of each model’s relative representation space to a high-performing reference model
Result: The correlation between performance and latent similarity was 0.955 (Pearson correlation), showing that relative representation similarity is a remarkably accurate proxy for model performance—without requiring any labeled data.

Training with Relative vs. Absolute Representations
Models trained end-to-end with relative representations achieve comparable performance to those trained with absolute representations:
Image Classification F1 Scores:
- MNIST: 97.91±0.07 (rel) vs. 97.95±0.10 (abs)
- Fashion-MNIST: 90.19±0.27 (rel) vs. 90.32±0.21 (abs)
- CIFAR-10: 87.70±0.09 (rel) vs. 87.85±0.06 (abs)
- CIFAR-100: 66.72±0.35 (rel) vs. 68.88±0.14 (abs)
Graph Node Classification F1 Scores:
- Cora: 0.89±0.02 (rel) vs. 0.90±0.01 (abs)
- CiteSeer: 0.77±0.03 (rel) vs. 0.78±0.03 (abs)
- PubMed: 0.91±0.01 (rel) vs. 0.91±0.01 (abs)
Zero-Shot Model Stitching
Relative representations enable zero-shot stitching of neural components without any training or fine-tuning.
Image Reconstruction
We trained autoencoders (AE) and variational autoencoders (VAE) with both absolute and relative representations across multiple datasets, then performed zero-shot stitching between encoders and decoders from different training runs.
Mean Squared Error (MSE) Results (averaged over 5 seeds):
| Model | Repr. | Type | MNIST | Fashion-MNIST | CIFAR-10 | CIFAR-100 | Mean |
|---|---|---|---|---|---|---|---|
| AE | Abs. | Non-Stitch | 0.66±0.02 | 1.57±0.03 | 1.94±0.08 | 2.13±0.08 | 1.58±0.05 |
| AE | Abs. | Stitch | 97.79±2.48 | 120.54±6.81 | 86.74±4.37 | 97.17±3.50 | 100.56±4.29 |
| AE | Rel. | Non-Stitch | 1.18±0.02 | 3.59±0.04 | 2.83±0.13 | 3.50±0.08 | 2.78±0.07 |
| AE | Rel. | Stitch | 2.83±0.20 | 6.37±0.29 | 5.39±1.18 | 18.03±12.46 | 8.16±3.53 |
Stitching with absolute representations produces up to two orders of magnitude higher error than non-stitched models. Relative representations reduce this gap dramatically, with stitched error only 2-5× higher than non-stitched.

Text Classification: Cross-Lingual Transfer
Using language-specific RoBERTa transformers for English, Spanish, French, and Japanese on Amazon Reviews sentiment classification:
F1 Scores (Coarse-grained, with Wikipedia anchors):
| Decoder | Encoder | Absolute | Relative |
|---|---|---|---|
| English | English | 91.54±0.58 | 90.45±0.52 |
| English | Spanish | 43.67±1.09 | 78.53±0.30 |
| English | French | 54.41±1.61 | 70.41±0.57 |
| English | Japanese | 48.72±0.90 | 66.31±0.80 |
This demonstrates zero-shot cross-lingual transfer: a classifier trained on English can make predictions on Spanish, French, or Japanese text with reasonable accuracy using relative representations, while absolute representations fail completely.
Text Classification: Cross-Architecture Transfer
Using different BERT variants (bert-base-cased, bert-base-uncased, ELECTRA, RoBERTa) on English text classification:
F1 Scores (averaged over 3 datasets):
| Type | TREC | DBpedia | Amazon Coarse |
|---|---|---|---|
| Non-Stitch (Abs.) | 91.70±1.39 | 98.62±0.58 | 87.81±1.58 |
| Stitch (Abs.) | 21.49±3.64 | 6.96±1.46 | 49.58±2.95 |
| Non-Stitch (Rel.) | 88.08±1.37 | 97.42±2.05 | 85.08±1.93 |
| Stitch (Rel.) | 75.89±5.38 | 80.47±21.14 | 72.37±7.32 |
Relative representations enable stitching across different transformer architectures, while absolute representations fail catastrophically.
Image Classification: Cross-Dataset Transfer
Using pre-trained vision transformers (ViT variants, RexNet) trained on ImageNet, with decoders trained on CIFAR-100:
F1 Scores (CIFAR-100 coarse-grained):
| Decoder | Encoder | Absolute | Relative |
|---|---|---|---|
| rexnet-100 | rexnet-100 | 82.06±0.15 | 80.22±0.28 |
| rexnet-100 | vit-base-patch16-224 | - | 76.81±0.49 |
| vit-base-patch16-224 | vit-base-patch16-224 | 93.15±0.05 | 91.94±0.10 |
| vit-base-patch16-224 | vit-base-resnet50-384 | 6.21±0.33 | 81.42±0.38 |
| vit-base-patch16-224 | vit-small-patch16-224 | - | 84.29±0.86 |
Remarkably, relative representations enable:
- Zero-shot transfer from ImageNet to CIFAR-100 using frozen encoders
- Stitching across different architectures with varying latent dimensions
- Performance degradation is modest (typically 5-15%) compared to matched encoder-decoder pairs
Key Findings
-
Angle preservation is pervasive: Across multiple modalities (images, text, graphs), architectures (CNNs, transformers, GNNs), and tasks (classification, reconstruction), neural networks trained on similar data produce latent spaces that preserve angles between embeddings.
- Relative representations enable zero-shot stitching: By encoding data relative to anchor points, we can stitch together encoders and decoders from:
- Different random seeds
- Different architectures (e.g., BERT variants, ViT variants)
- Different languages (English, Spanish, French, Japanese)
- Different datasets (ImageNet → CIFAR)
-
Latent similarity predicts performance: The similarity between relative representations of two models correlates strongly (r=0.955) with their relative performance, providing a differentiable, label-free metric for model evaluation.
-
Training with relative representations is effective: End-to-end training with relative representations achieves comparable performance to standard absolute representations, showing the approach is practical for real applications.
- Anchors are key: The number and diversity of anchors affect representation quality. More anchors generally improve frozen-encoder performance, though the optimal strategy depends on the task.
Citation
@inproceedings{moschella2023relative,
title = {Relative representations enable zero-shot latent space communication},
author = {Moschella, Luca and Maiorca, Valentino and Fumero, Marco and
Norelli, Antonio and Locatello, Francesco and Rodol{\`a}, Emanuele},
booktitle = {The Eleventh International Conference on Learning Representations},
year = {2023},
url = {https://openreview.net/forum?id=SrC-nwieGJ}
}
Authors
Luca Moschella¹’* · Valentino Maiorca¹’* · Marco Fumero¹ · Antonio Norelli¹ · Francesco Locatello²’† · Emanuele Rodolà¹
¹Sapienza University of Rome · ²Amazon Web Services
*Equal contribution · †Work done outside of Amazon
Limitations and Future Directions
-
Similarity functions: While cosine similarity works well, other functions could enforce different invariances (e.g., to non-isometric deformations with bounded distortion)
-
Anchor selection: The relationship between anchor composition and representation expressivity requires further investigation. Optimal strategies may vary by task and domain.
-
Computational cost: Training cost depends on the number of anchors and their update frequency
-
Geodesic distances: Using geodesic distances over the data manifold instead of Euclidean approximations could improve representation quality
-
Multi-layer stitching: Extending the approach to stitch multiple layers could enable more modular, reusable network components