Overview
Reinforcement learning agents typically fail when deployed in environments with even minor perceptual variations from their training conditions. An agent trained to drive on green grass will fail on red grass, despite the task being identical. This brittleness stems from a fundamental limitation: encoders trained in different visual contexts produce incompatible latent representations, making it impossible to reuse learned components.
R3L (Relative Representations for Reinforcement Learning) solves this by transforming absolute encoder outputs into a coordinate-free space where representations are defined relative to anchor points rather than in arbitrary coordinate systems. This enables unprecedented compositional generalization: encoders and controllers trained independently across different visual variations and task objectives can be stitched together zero-shot, without any fine-tuning.
The result? Train N visual variations and M task variations separately (N+M models), then compose them to obtain N×M agents—achieving 75% reduction in training time while maintaining performance comparable to end-to-end training.
Method: Coordinate-Free Representations for RL
The Problem: Incompatible Latent Spaces
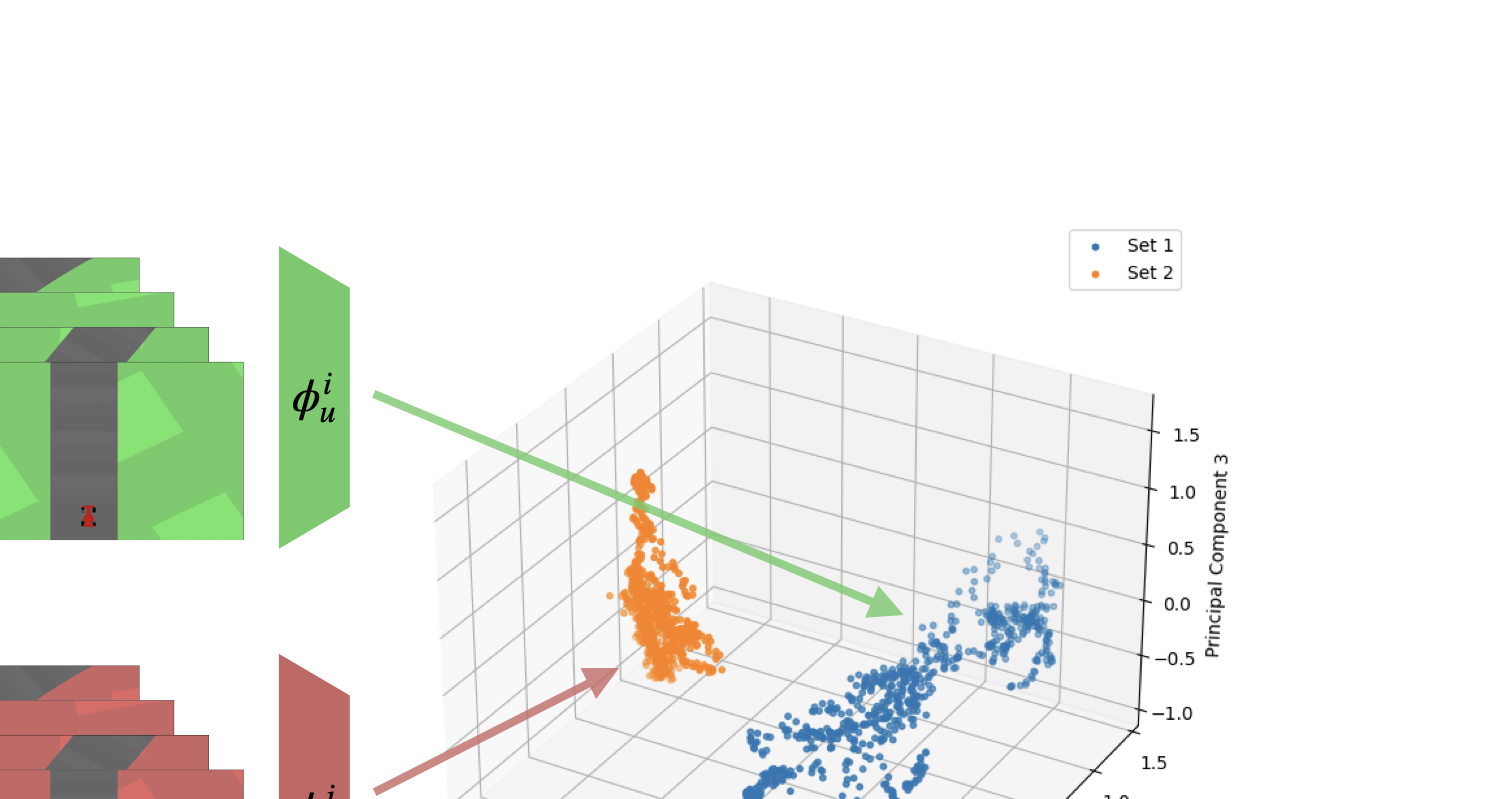
When two RL agents are trained independently on perceptually different environments (e.g., green vs red background), their encoders learn semantically similar but coordinate-wise incompatible representations. Even when observing aligned frames showing the same semantic content, the encoder outputs occupy completely separate regions of the latent space.
This is analogous to two cartographers mapping the same territory using different projections—the maps describe the same reality but cannot be overlaid due to arbitrary coordinate choices.
The Solution: Relative Representations
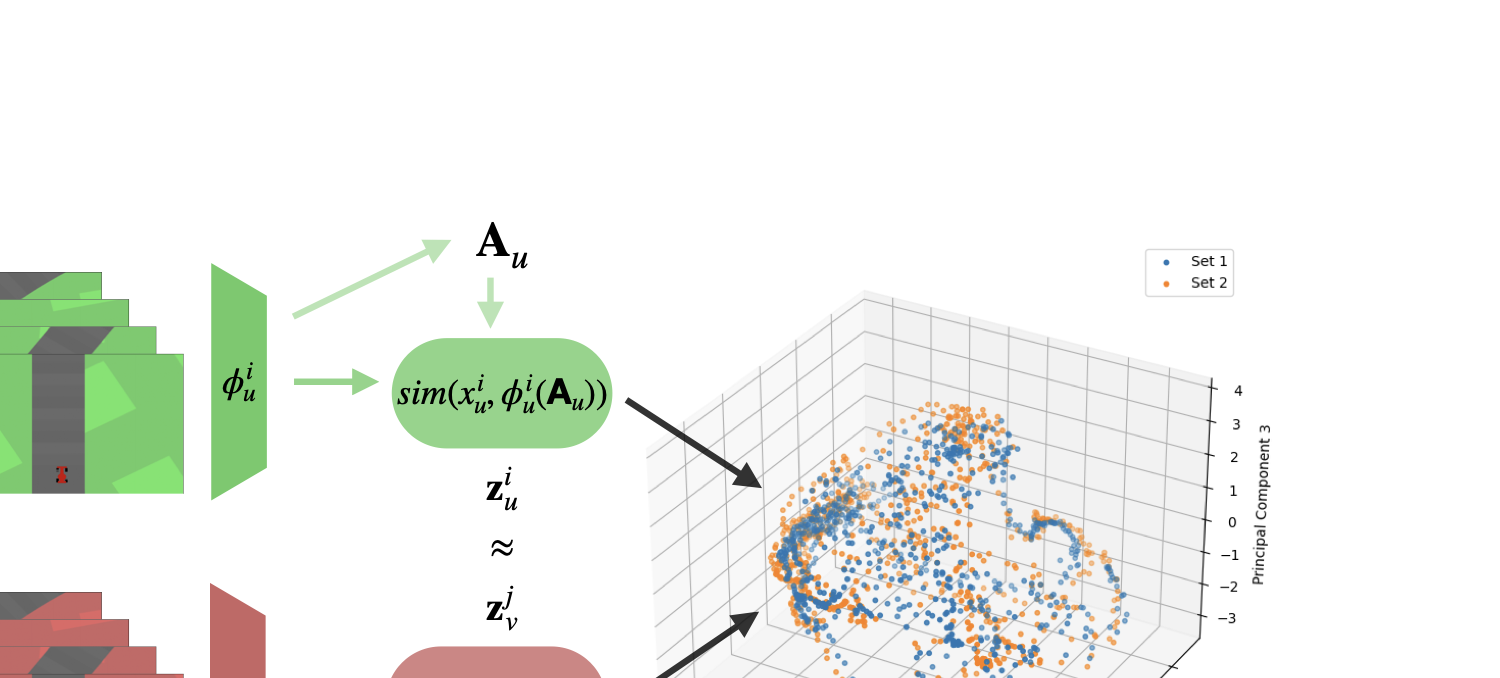
R3L adapts the relative representations framework from representation learning to the RL setting. Instead of using raw encoder embeddings \(\phi(s)\), we express them relative to a set of anchor points \(\mathcal{A} = \{A_1, \ldots, A_K\}\):
\[\psi(s) = \left[ d(\phi(s), \phi(A_1)), \ldots, d(\phi(s), \phi(A_K)) \right]\]where \(d(\cdot, \cdot)\) is a distance metric (we use cosine distance). This coordinate-free representation:
- Removes arbitrary rotations/translations: Only relative distances matter, not absolute coordinates
- Aligns latent spaces: Encoders trained independently produce comparable relative representations
- Enables composition: Controllers can operate on any encoder’s relative space
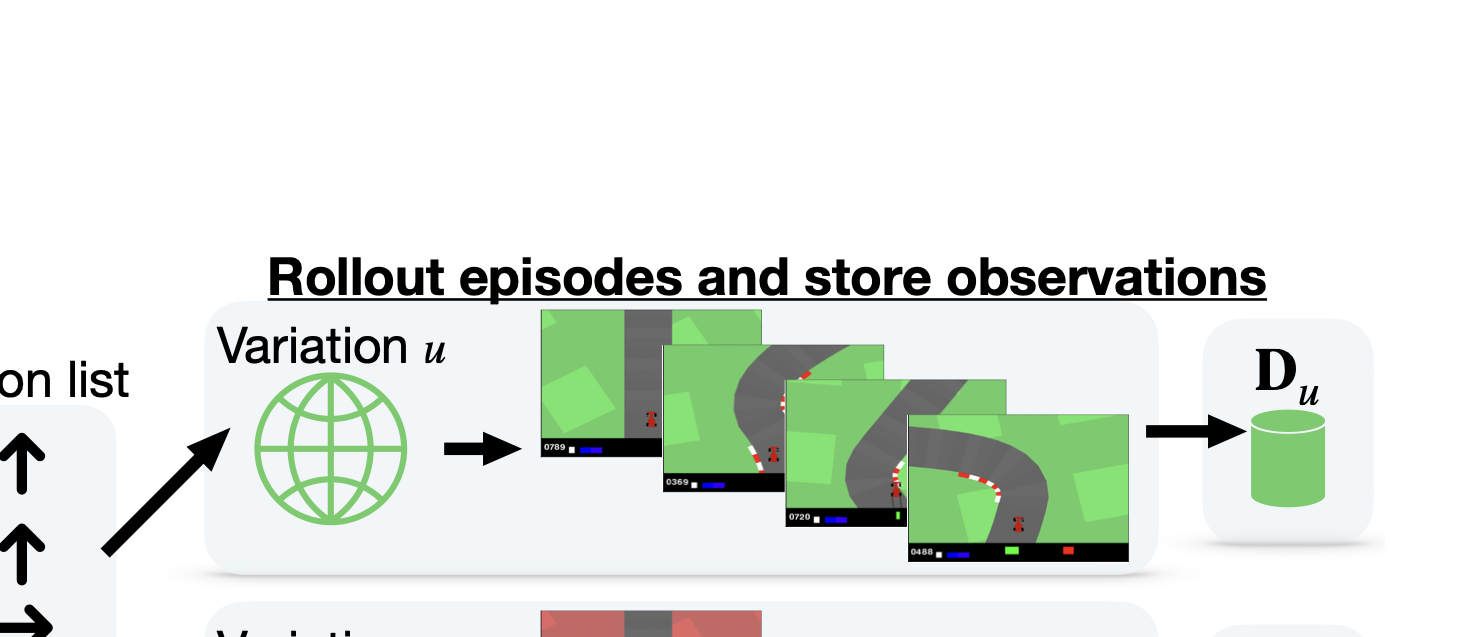
Anchor Collection and Stabilization
Anchors are collected by playing identical action sequences in both environment variations, ensuring corresponding observations are aligned. During training, we use Exponential Moving Average (EMA) to stabilize anchor embeddings:
\[\phi(A_t) = \alpha \cdot \phi(A_t) + (1 - \alpha) \cdot \phi(A_{t-1})\]This prevents chaotic shifts in the relative coordinate system as the encoder evolves during training. We use \(\alpha = 0.999\) for all experiments.
Latent Space Alignment Analysis
To verify that relative representations successfully align latent spaces, we analyze pairwise cosine similarities between ~800 aligned frames from two CarRacing environments (green vs red grass).


Key insight: Relative representations reveal quasi-isometric structure—independently trained encoders learn the same semantic content in different coordinate systems, which R3L makes invariant.
Zero-Shot Stitching Results
The core contribution of R3L is enabling modular composition of RL agents through zero-shot stitching: combining encoders and controllers trained independently without any fine-tuning.
CarRacing: Visual and Task Variations
We train separate encoders for 4 visual variations (green/red/blue grass, far camera) and separate controllers for 4 task variations (standard, slow, scrambled actions, no-idle). Each encoder-controller pair can be stitched to create 16 different agents.
| Encoder | Method | Green | Red | Blue | Slow | Scrambled | No-idle |
|---|---|---|---|---|---|---|---|
| Green | S.Abs (naive) | 175±304 | 167±226 | -4±79 | 148±328 | 106±217 | 213±201 |
| S.R3L (ours) | 781±108 | 787±62 | 794±61 | 268±14 | 781±126 | 824±82 | |
| Red | S.Abs (naive) | 157±248 | 43±205 | 22±112 | 83±191 | 138±244 | 252±228 |
| S.R3L (ours) | 810±52 | 776±92 | 803±58 | 476±430 | 790±72 | 817±69 | |
| Blue | S.Abs (naive) | 137±225 | 130±274 | 11±122 | 95±128 | 138±224 | 144±206 |
| S.R3L (ours) | 791±64 | 793±40 | 792±48 | 564±440 | 804±41 | 828±50 |
Training Time Savings
Train all 16 visual-task combinations independently
52 hours
Complexity: O(V×T)Train only 4+4 models (diagonal), stitch the rest
13 hours
Complexity: O(V+T)| V1 (green) | V2 (red) | V3 (blue) | V4 (far) | |
|---|---|---|---|---|
| T1 (standard) | 3h | - | - | - |
| T2 (slow) | - | 4h | - | - |
| T3 (no-idle) | - | - | 3h | - |
| T4 (scrambled) | - | - | - | 3h |
Training Dynamics
To verify that relative representations maintain training stability, we visualize learning curves across CarRacing and Atari environments. The plots show that R3L training converges smoothly without instability from the coordinate transformation.
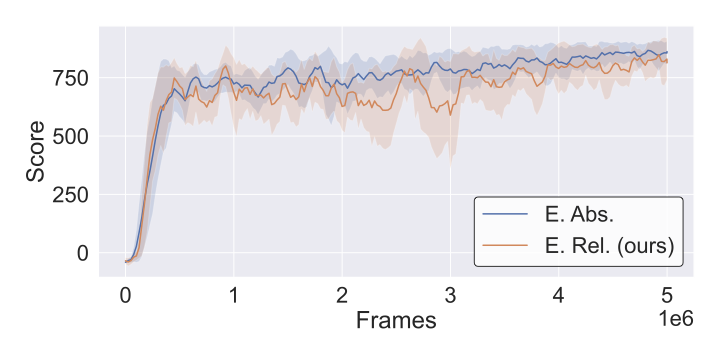
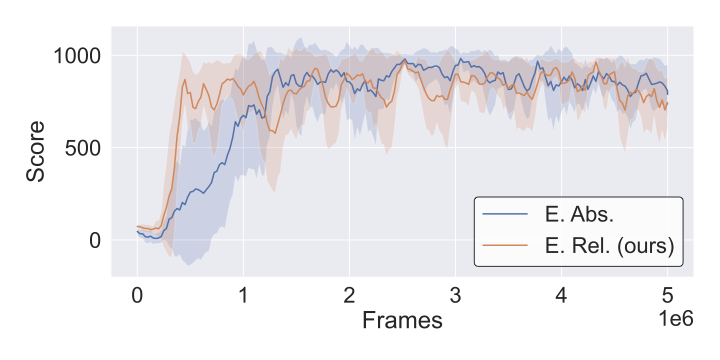
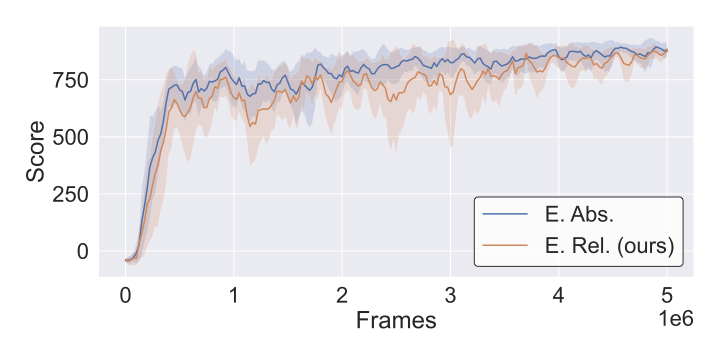
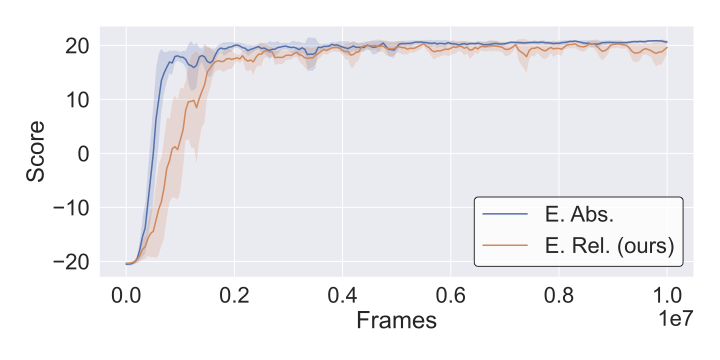
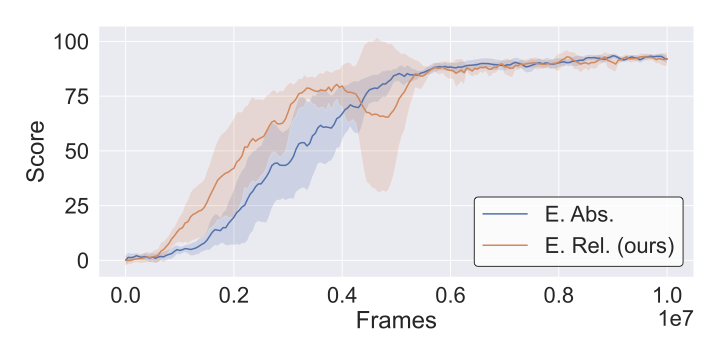
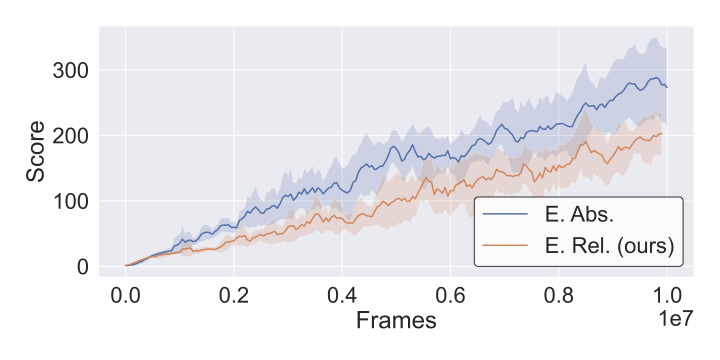
Key observation: All training curves show stable convergence patterns comparable to standard absolute training. The relative encoding does not introduce training instabilities or convergence issues, validating that coordinate-free representations are compatible with standard RL optimization procedures.
EMA Stabilization Analysis
Anchor embeddings evolve during training as the encoder learns. To prevent chaotic shifts in the relative coordinate system, we stabilize anchors using Exponential Moving Average (EMA). Below we compare different EMA coefficients:
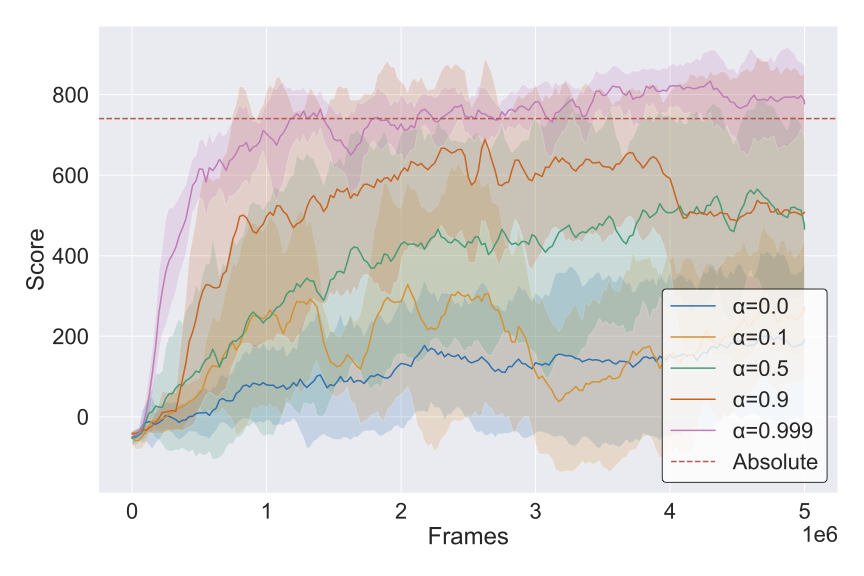
The EMA update formula is:
\[\phi(A_t) = \alpha \cdot \phi(A_t) + (1 - \alpha) \cdot \phi(A_{t-1})\]With α=0.999, anchors update slowly, providing a stable coordinate frame while allowing gradual adaptation as the encoder improves. This is analogous to temperature control in alchemical transmutation—too fast and the structure collapses, too slow and transformation stalls.
Environment Visualizations
R3L enables composition across diverse visual variations. Below are examples of the different CarRacing environment appearances used in our experiments:

These perceptually different environments produce incompatible latent spaces when using standard encoders, but R3L’s relative representations enable seamless stitching of components trained on different variations.
Atari Experiments
We test generalization beyond CarRacing on three Atari games (Pong, Boxing, Breakout) with background color variations to evaluate R3L on precision-critical, frame-perfect environments.
| Game | Variation | E.Abs | E.R3L | Status |
|---|---|---|---|---|
| Pong | Plain/Green/Red | 21±0 | 20-21±0 | Perfect |
| Boxing | Plain/Green/Red | 95-96±2 | 88-95±4 | Competitive |
| Breakout | Plain/Green/Red | 132-298±60 | 77-146±60 | Degraded |
Pong
Perfect performance maintained (21/21). Simple visual structure enables complete preservation of task-relevant information.
Boxing
Slight degradation but competitive. Moderate visual complexity handled well by relative representations.
Breakout
Significant performance drop. Numerous bricks create detailed patterns that may lose fine-grained spatial information in coordinate transformation.
Key Findings
RL encoders trained independently on visual variations learn semantically aligned representations obscured only by arbitrary coordinate differences—a structure that relative representations make invariant.
Like different map projections of the same territory
Stitching encoders and controllers across visual and task variations achieves 4-10× improvement over naive composition, approaching end-to-end performance on visual variations (750-830 vs 800-850).
Training complexity reduces from O(V×T) to O(V+T), achieving 75% time savings that scale with variation diversity.
From multiplicative to additive scaling
Temporal/dynamic variations (slow task: 268-564 vs E.Abs 996) and visually complex scenes (Breakout) expose limitations, suggesting coordinate transformation may lose fine-grained information.
Relative encoding does not compromise RL training dynamics—convergence and stability match standard absolute training across all environments. The coordinate-free transformation integrates seamlessly with standard RL optimization procedures.
Citation
@misc{ricciardi2025r3l,
title = {R3L: Relative Representations for Reinforcement Learning},
author = {Antonio Pio Ricciardi and Valentino Maiorca and Luca Moschella and
Riccardo Marin and Emanuele Rodolà},
year = {2025},
eprint = {2404.12917},
archiveprefix = {arXiv},
primaryclass = {cs.LG},
url = {https://arxiv.org/abs/2404.12917}
}
Authors
Antonio Pio Ricciardi¹ · Valentino Maiorca¹’² · Luca Moschella¹ · Riccardo Marin³ · Emanuele Rodolà¹
¹Sapienza University of Rome, Italy · ²Institute of Science and Technology Austria (ISTA) · ³University of Tübingen, Germany