Latent Functional Maps

A spectral framework for representation alignment

NeurIPS 2024

TL;DR: We adapt the functional maps framework from 3D geometry processing to neural latent spaces by computing spectral transformations between graph Laplacian eigenbases. This provides a unified framework that can compare representational spaces, find correspondences with minimal supervision (5-10 anchors), and transfer representations while maintaining interpretability through spectral analysis.

Overview

Neural networks learn data representations that lie on low-dimensional manifolds, yet modeling the relationship between these representational spaces remains an ongoing challenge. Latent Functional Maps (LFM) introduces a spectral framework that addresses this problem in the functional domain, bringing together principles from spectral geometry and representation learning.

By adapting the functional maps framework from 3D geometry processing to neural latent spaces, LFM provides a versatile tool that enables three key capabilities:

Compare different representational spaces in an interpretable way and measure their intrinsic similarity
Find correspondences between spaces, both in unsupervised and weakly supervised settings
Transfer representations effectively between distinct spaces

Framework overview: Given two spaces X and Y, their samples lie on manifolds M and N, approximated with k-NN graphs. We optimize for a latent functional map C between the eigenbases of operators defined on the graphs. This map serves as a transformation between functions defined on the two manifolds and can be leveraged for (i) comparing representational spaces, (ii) solving correspondence problems, and (iii) transferring information between spaces.

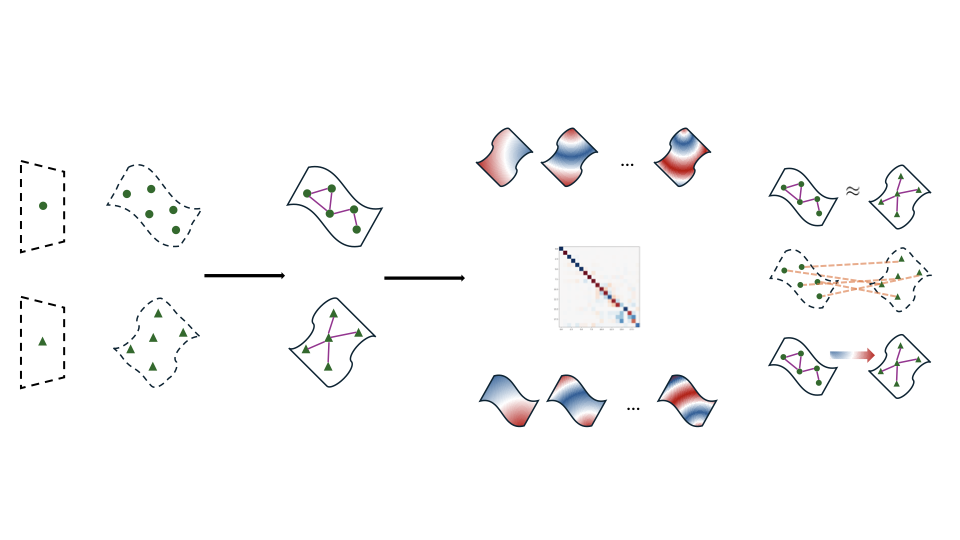
Spectral Framework: From Geometry to Representation Learning

Building the Graph Representation

To leverage the geometry of the underlying manifold, LFM models the latent space by constructing a symmetric k-nearest neighbor (k-NN) graph. Given samples \(X = \{x_1, \ldots, x_n\}\) from a latent space \(\mathcal{X}\), we build an undirected weighted graph \(G = (X, E, \mathbf{W})\) where edges connect nearby points in the latent space.

We then compute the graph Laplacian \(\mathcal{L}_G = \mathbf{I} - \mathbf{D}^{-1/2} \mathbf{W} \mathbf{D}^{-1/2}\) and its eigendecomposition \(\mathcal{L}_G = \mathbf{\Phi}_G \mathbf{\Lambda}_G \mathbf{\Phi}_G^T\). The eigenvectors \(\mathbf{\Phi}_G\) form an orthonormal basis for functions defined on the graph, providing a spectral representation of the latent space.

Computing Latent Functional Maps

Given two latent spaces \(\mathcal{X}\) and \(\mathcal{Y}\) with their graph Laplacians and eigenbases, we compute a functional map \(\mathbf{C}\) that transforms functions between these spaces. The optimization problem is:

\[\underset{\mathbf{C}}{\mathrm{argmin}} \| \mathbf{C} \hat{\mathbf{F}}_{G_X}- \hat{\mathbf{F}}_{G_Y} \|_F^2 + \alpha \rho_{\mathcal{L}}(\mathbf{C}) + \beta \rho_{f}(\mathbf{C})\]

where \(\hat{\mathbf{F}}_G = \mathbf{\Phi}_{G}^T \mathbf{F}_G\) are the spectral coefficients of descriptor functions \(\mathbf{F}_G\), and \(\rho_{\mathcal{L}}\), \(\rho_{f}\) are regularizers enforcing Laplacian and descriptor commutativity.

Descriptor Functions

Descriptors encode information shared between spaces \(\mathcal{X}\) and \(\mathcal{Y}\):

Supervised: Distance functions from known anchor points (partial correspondences)
Weakly supervised: Equivalence relations like label assignments (multi-to-multi mappings)
Unsupervised: Geometric quantities that depend only on the graph topology (e.g., Heat Kernel Signature)

This flexibility allows LFM to work with varying amounts of supervision, from zero anchors to full correspondence information.

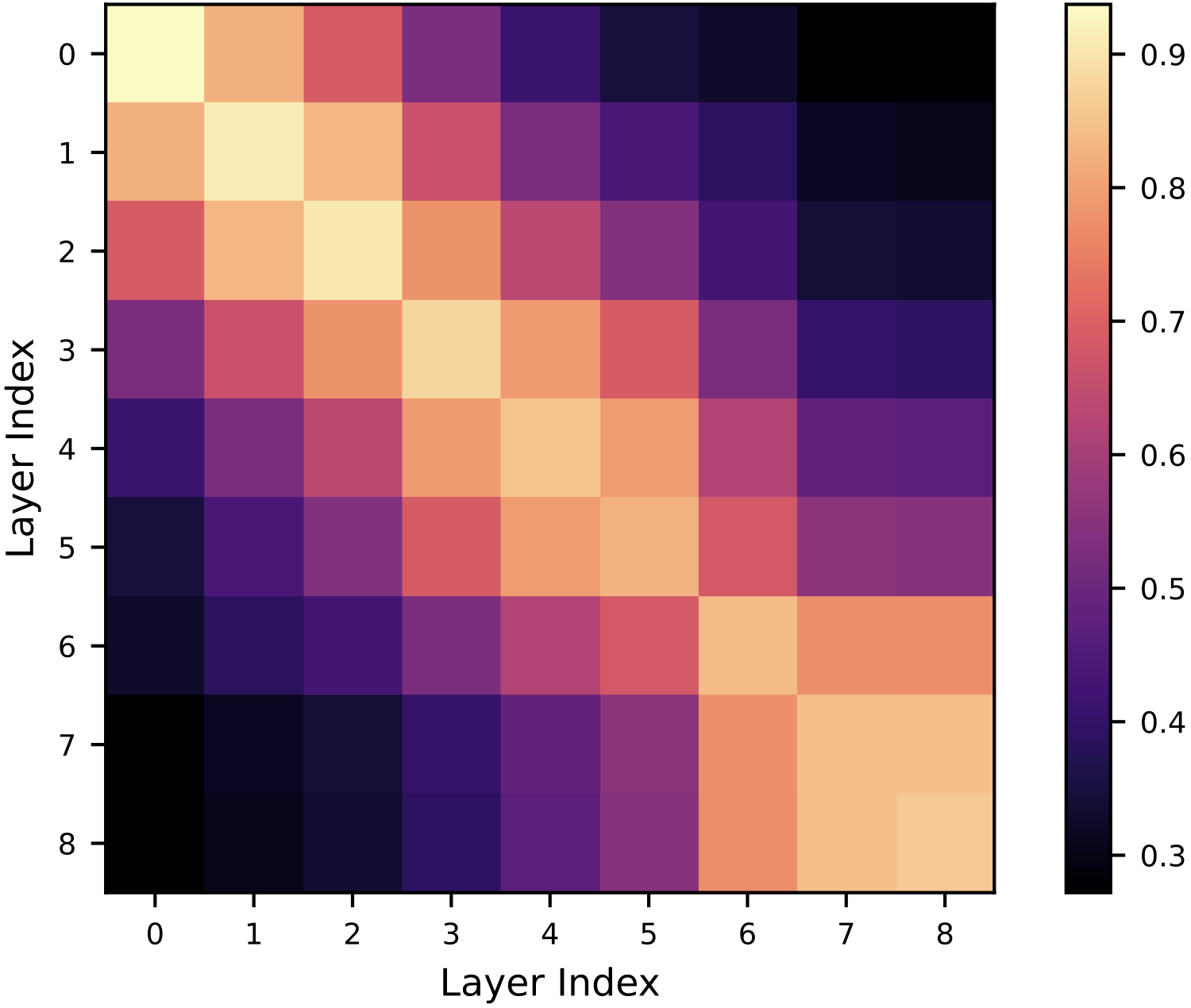
LFM as an Interpretable Similarity Measure

The functional map \(\mathbf{C}\) itself provides a meaningful similarity measure between spaces. For isometric transformations, the functional map is volume-preserving, manifested in an orthogonal \(\mathbf{C}\). We define similarity as:

\[\text{sim}(X,Y) = 1 - \frac{\|\text{off}(\mathbf{C}^T\mathbf{C})\|_F^2}{\|\mathbf{C}^T\mathbf{C}\|_F^2}\]

This metric is not only more robust than existing methods like CKA (Centered Kernel Alignment) but also interpretable: the eigenvectors of \(\mathbf{C}^T\mathbf{C}\) localize regions of high distortion in the target manifold.

Left: Similarity matrix between CIFAR-10 layers using LFM (99.8% accuracy matching corresponding layers). Right: Robustness comparison - LFM similarity remains stable under perturbations that preserve linear separability, while CKA degrades.

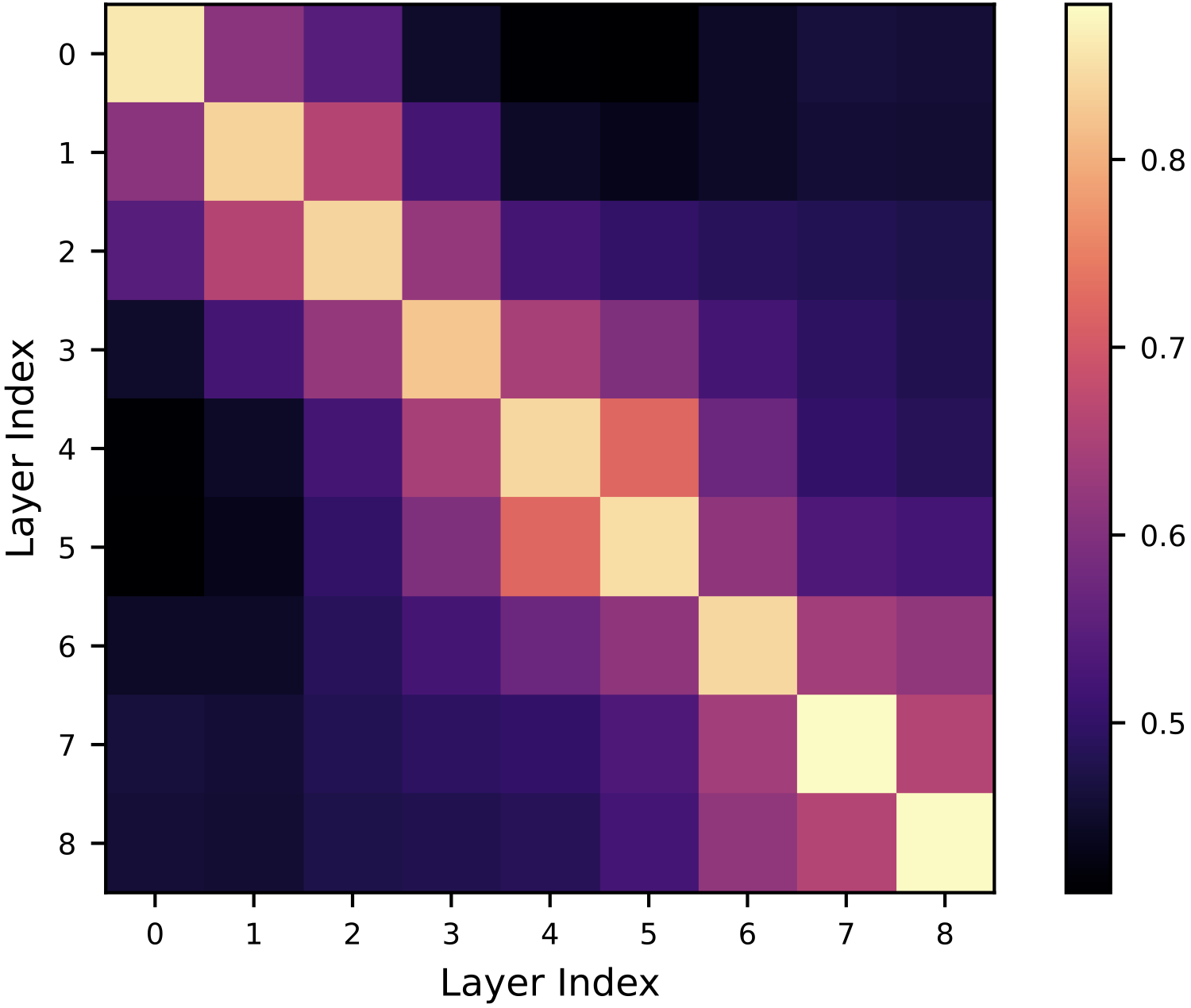
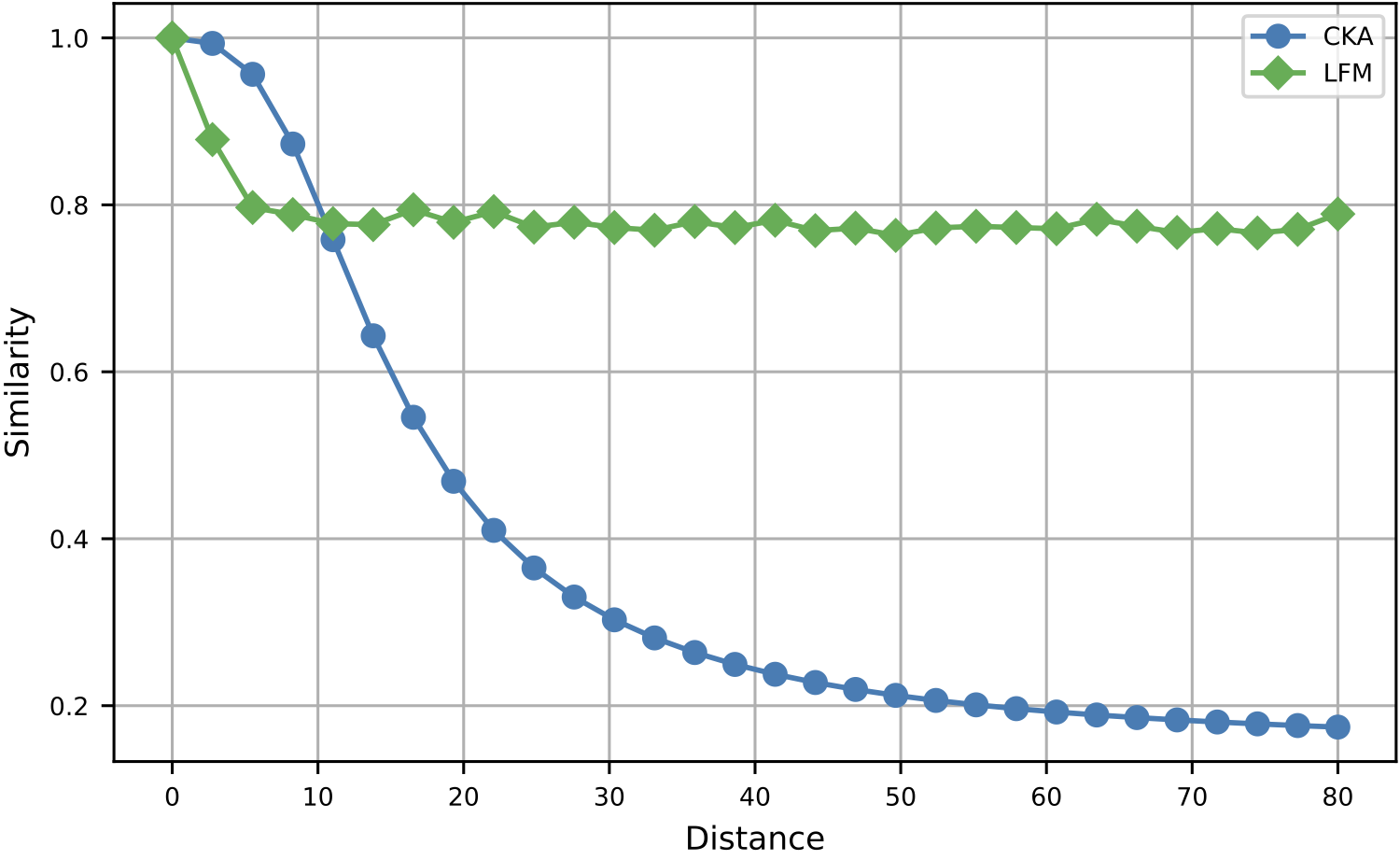
Robustness to Semantically Preserving Transformations

A critical advantage of LFM is its robustness to transformations that preserve the semantic structure of representations. When latent representations are perturbed in directions orthogonal to the decision boundary (preserving linear separability), LFM similarity scores remain high while CKA degrades significantly. This demonstrates that LFM better captures the task-relevant structure of representations.

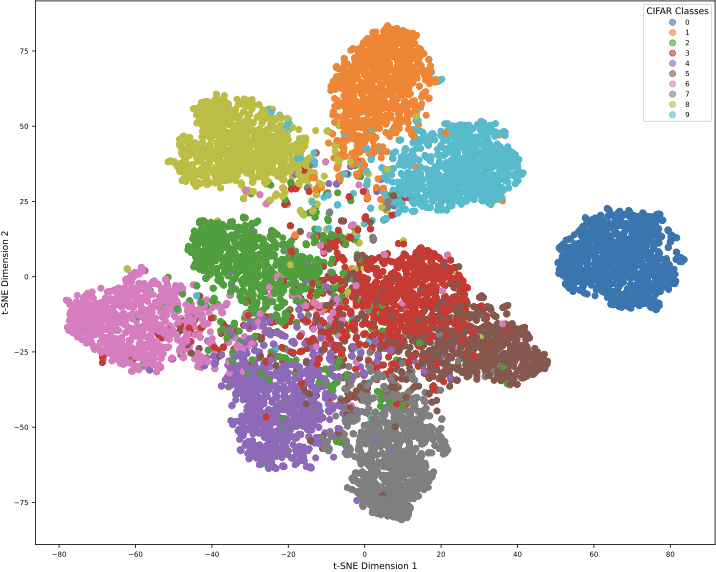
t-SNE visualization of CIFAR-10 latent space

Left: CKA similarity matrix for comparison. Right: t-SNE visualization showing the geometric structure of CIFAR-10 representations in the latent space.

Experiments and Results

Zero-Shot Stitching

In latent communication tasks, a common challenge is combining an encoder from one model with a decoder from another without any training. LFM enables truly zero-shot stitching - no training, fine-tuning, or pre-trained stitching layers required.

Stitching accuracy on CIFAR-100 with varying numbers of anchor points. LFM+Ortho consistently outperforms direct orthogonal transformation, especially with few anchors. LFM+Ortho (Labels) uses only dataset labels as descriptors, requiring no anchors at all.

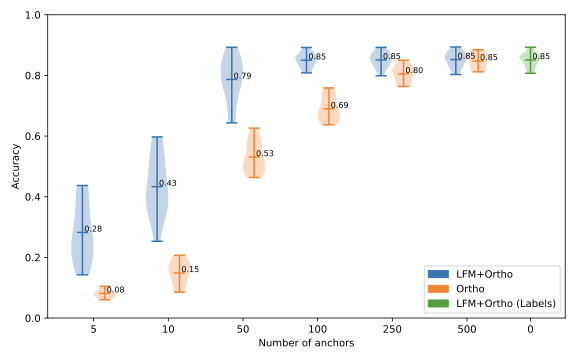
Key findings:

With just 5-10 anchors, LFM achieves performance comparable to methods using 50+ anchors
Using only dataset labels (no anchors), LFM achieves strong zero-shot stitching performance
Results validated across multiple datasets: CIFAR-100, ImageNet, CUB, MNIST, and AgNews
Works across modalities: both vision and text encoders

Retrieval Tasks

LFM significantly improves retrieval performance when aligning word embeddings from different models (FastText and Word2Vec):

Mean Reciprocal Rank (MRR) for word embedding retrieval as a function of anchor count. LFM achieves MRR > 0.8 with just 5 anchors and reaches 0.99 with 300 anchors, substantially outperforming baseline methods.

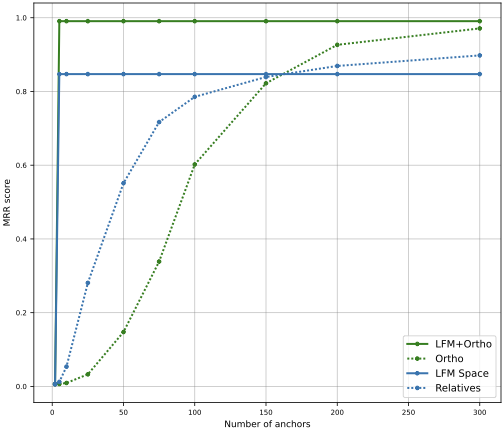
Key findings:

With 5 anchors, LFM achieves MRR > 0.8, while baselines remain below 0.4
Performance plateaus around 25-50 eigenvectors, indicating this is sufficient for optimal alignment
The functional representation provides an interpretable intermediate space for alignment

Visualizing Functional Maps

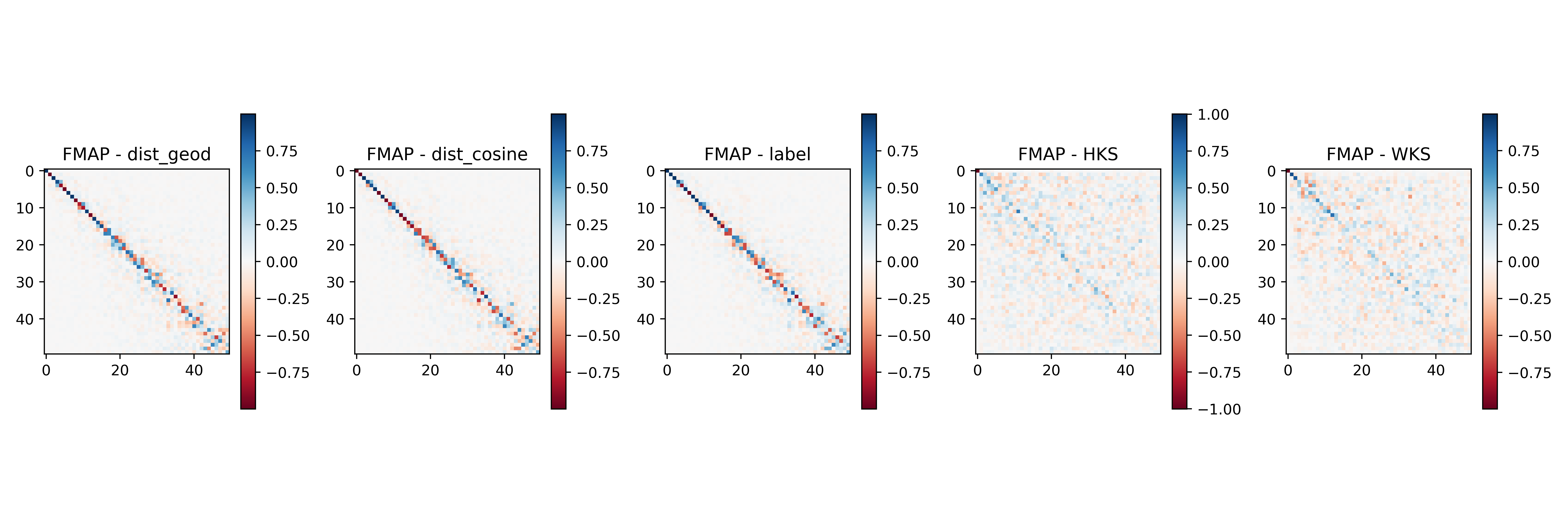
Visualization of functional map matrices between MNIST latent spaces. The diagonal-dominant structure with smooth off-diagonal decay indicates near-isometric alignment, with most information concentrated in low-frequency components.

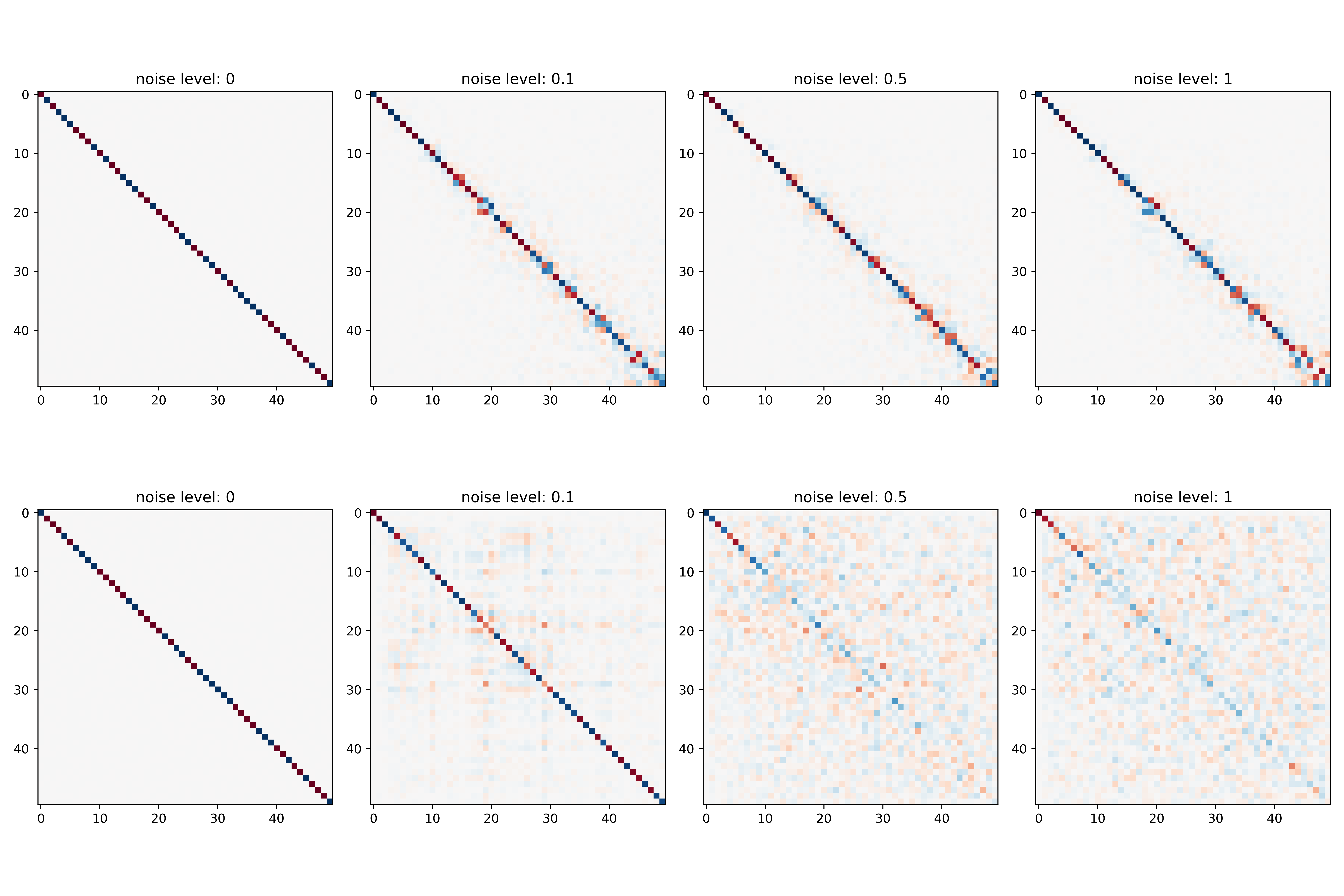
Functional maps under noise perturbations

Robustness of functional maps: visualization showing how functional maps remain stable and preserve structure even under noise perturbations, demonstrating the spectral framework's resilience to variations in the input space.

Functional Space Visualization

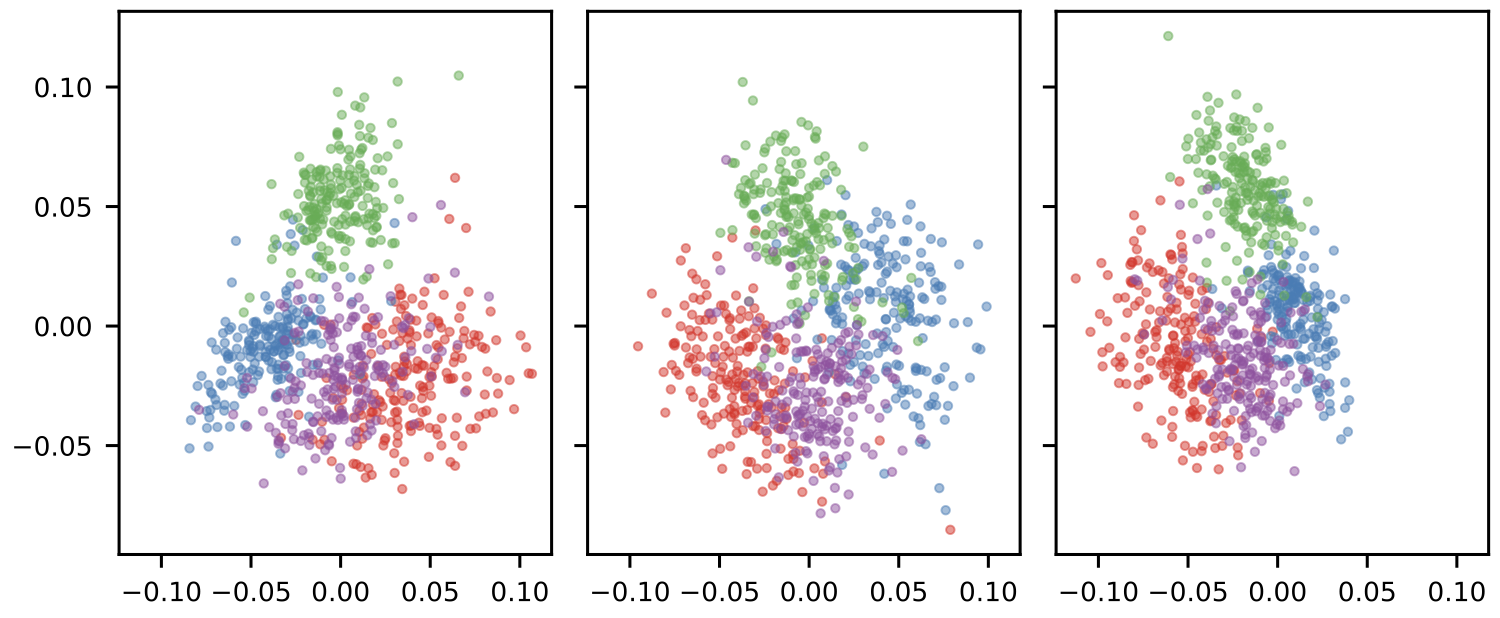
Left: Functional space representation showing the alignment quality in the spectral domain. Right: Translation space visualization demonstrating how correspondences are established between different representational spaces through the functional map framework.

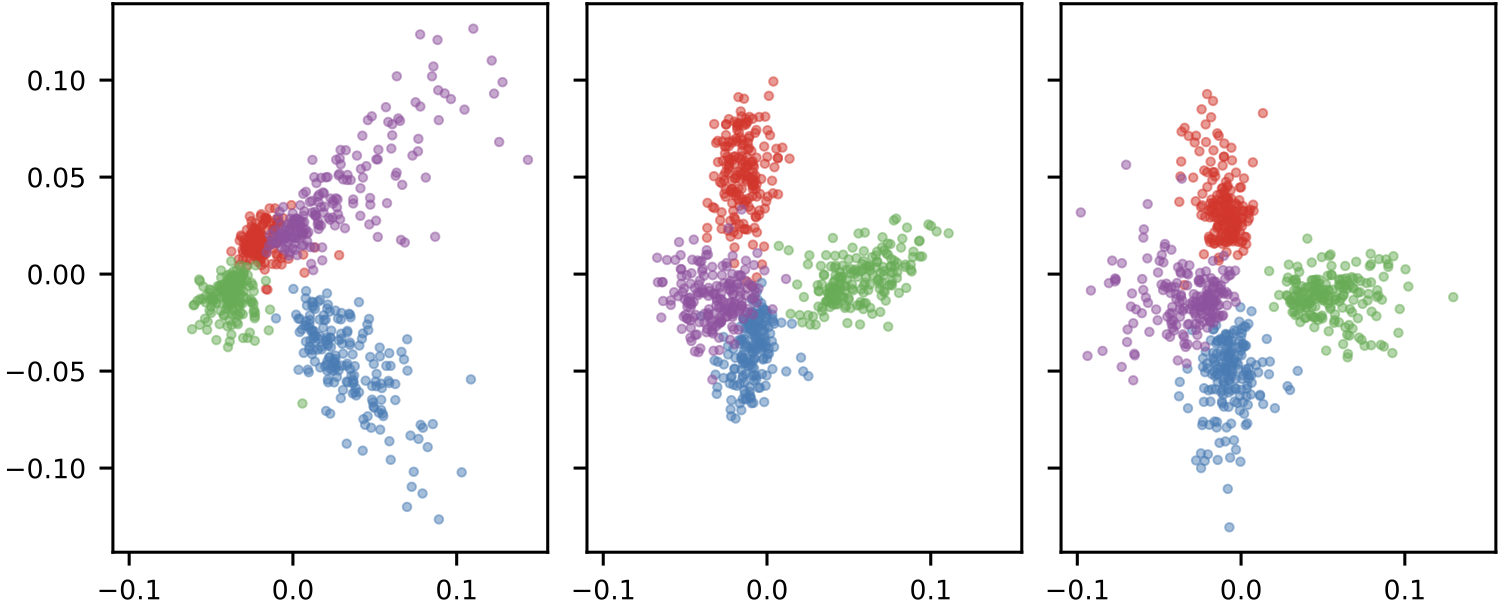
Autoencoder Stitching Applications

LFM enables cross-model autoencoder stitching, where an encoder from one model can be combined with a decoder from another to reconstruct inputs. This demonstrates the framework’s ability to align representational spaces across different architectures.

Zero-shot autoencoder stitching results. Left: MNIST reconstructions using cross-model encoder-decoder pairs aligned via LFM. Right: CIFAR-10 reconstructions demonstrating successful alignment across color images with more complex structures. The framework preserves semantic content while bridging different latent representations.

Key Findings

Spectral methods are effective for latent alignment: By working in the functional domain rather than the point domain, LFM simplifies complex alignment problems while enhancing interpretability.
Sample efficiency: LFM requires orders of magnitude fewer correspondences (5-10 anchors) compared to traditional methods to achieve strong alignment performance.
Multi-purpose framework: Unlike previous methods that address only one aspect of alignment, LFM provides a unified framework for similarity measurement, correspondence finding, and representation transfer.
Interpretability: The functional map structure reveals the spectral relationship between spaces, localizes distortions, and provides insights into which frequencies capture task-relevant information.
Robustness: LFM is stable to transformations that preserve the semantic structure of representations, making it more reliable than kernel-based methods like CKA.
Modality-agnostic: Validated across vision (CNNs, ViTs, DINO) and language (word embeddings) domains, demonstrating broad applicability.

Citation

@inproceedings{fumero2024latent,
  title     = {Latent Functional Maps: a spectral framework for representation alignment},
  author    = {Fumero*, Marco and Pegoraro*, Marco and Maiorca, Valentino and
               Locatello, Francesco and Rodol{\`a}, Emanuele},
  booktitle = {Advances in Neural Information Processing Systems},
  year      = {2024}
}

Authors

Marco Fumero¹* · Marco Pegoraro²* · Valentino Maiorca² · Francesco Locatello¹ · Emanuele Rodola²

¹Institute of Science and Technology Austria · ²Sapienza University of Rome

*Equal contribution

Research Impact: This work bridges spectral geometry and deep learning, demonstrating how classical tools from geometry can be adapted to solve modern representation learning challenges. The framework's versatility makes it applicable to model stitching, transfer learning, multi-modal alignment, and interpretability research.