TL;DR
We formalize the inverse transformation from relative space back to absolute space, enabling zero-shot latent space translation without concurrent access to both models or additional training. Combined with the scale invariance properties of neural classifiers, this enables practical model compositionality where pre-trained encoders and classifiers can be mixed and matched across architectures and modalities.
Overview
Neural networks trained independently on similar data develop representations that differ by transformations such as rotations or rescaling, despite capturing equivalent semantic information. Inverse Relative Projection (IRP) provides a solution to communicate between these latent spaces without requiring concurrent access to both models or any additional training.
Our method combines three key insights: (1) the invertibility of angle-preserving relative representations, (2) the scale invariance of neural network decoders, and (3) the well-behaved Gaussian distribution of embedding scales. Together, these enable zero-shot translation between arbitrary latent spaces by using a shared relative space as an intermediary.
This approach has significant practical implications: it enables model compositionality, allowing pre-trained encoders and classifiers to be mixed and matched even when trained independently on different datasets or modalities.
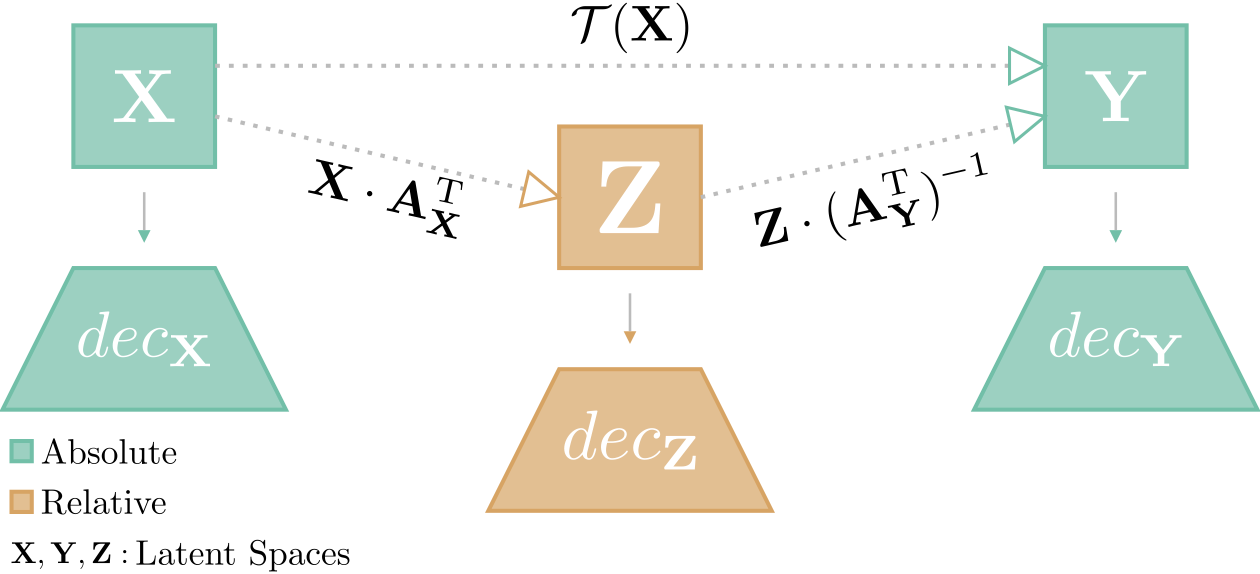
Method: Inverting Relative Representations
Relative Representations as a Bridge
Relative representations, introduced by Moschella et al., represent samples not in absolute coordinates but relative to a set of anchor points. For a latent space $\mathcal{X} \subset \mathbb{R}^d$ with anchors $\mathcal{A}_{\mathcal{X}}$, this is formalized as:
\[\mathbf{X}_{rel} = \mathbf{X}_{abs} \cdot \mathbf{A}_{\mathcal{X}}^T\]where samples are normalized to unit norm before projection. This captures the intrinsic shape of the data by considering only the relative angles between points, completely discarding scale information.
The key insight is that semantically similar latent spaces, when projected using parallel anchors (i.e., anchors in semantic correspondence), produce nearly identical relative representations: $\mathbf{X}{rel} \approx \mathbf{Y}{rel}$.
The Core Contribution: Inverse Projection
Our central contribution is formalizing the inverse transformation from relative space back to absolute space:
\[\mathbf{Y}_{abs} = \mathbf{X}_{rel} \cdot (\mathbf{A}_{\mathcal{Y}}^T)^{-1}\]This allows us to decode from the relative space into any target absolute space $\mathcal{Y}$ using only the anchors from $\mathcal{Y}$. The translation pipeline becomes:
- Encode: Project from source space $\mathcal{X}$ to relative space using $\mathbf{A}_{\mathcal{X}}$
- Bridge: Leverage the property that $\mathbf{X}{rel} \approx \mathbf{Y}{rel}$ for semantically similar spaces
- Decode: Project from relative space to target space $\mathcal{Y}$ using $\mathbf{A}_{\mathcal{Y}}$
Critically, the encoding and decoding steps are independent: each space can be mapped to or from the relative space without knowledge of other spaces, enabling true zero-shot compositionality.
Stability Improvements
Computing the inverse of the anchor matrix can be unstable when anchors are correlated. We introduce three techniques to improve robustness:
Anchor Pruning: Use farthest point sampling (FPS) with a customized cosine distance to select maximally orthogonal anchors:
\[\mathrm{dcos}(\mathbf{X}) = 1 - \left|\frac{\mathbf{X} \cdot \mathbf{X}^T}{\|\mathbf{X}\|^2}\right|\]where the absolute value prevents selecting quasi-colinear points with opposite directions.
Anchor Subspaces: Apply pruning multiple times with different random seeds ($\omega$ times), reconstructing the absolute space independently for each subspace, then average-pool the results:
\[\mathbf{Y}_{abs} = \frac{1}{\omega} \sum_{i=1}^{\omega} \mathbf{X}_{rel} \cdot (\mathbf{S}_{\mathcal{Y}}^{i\,T})^{-1}\]This ensemble approach balances stability with information coverage.
Anchor Completion: Encode the identity matrix using a pruned anchor subset and decode it with the full anchor set, effectively estimating the rotation and reflection matrix while stabilizing computation.
Scale Invariance: The Missing Piece
A fundamental challenge in inverting relative representations is that they discard scale information. We demonstrate that neural classifiers exhibit surprising scale invariance properties, allowing us to ignore the exact scale when decoding.
Theoretical Foundation
The softmax function used in neural classifiers is inherently scale-invariant up to temperature:
\[\operatorname{softmax}(x)_i = \frac{e^{y_i/T}}{\sum_j e^{y_j/T}}\]A rescaling factor $\alpha$ applied to the input can be factored through linear layers: $\mathbf{y} = \alpha \mathbf{W}\mathbf{x} + b$, becoming equivalent to a temperature adjustment at the softmax level.
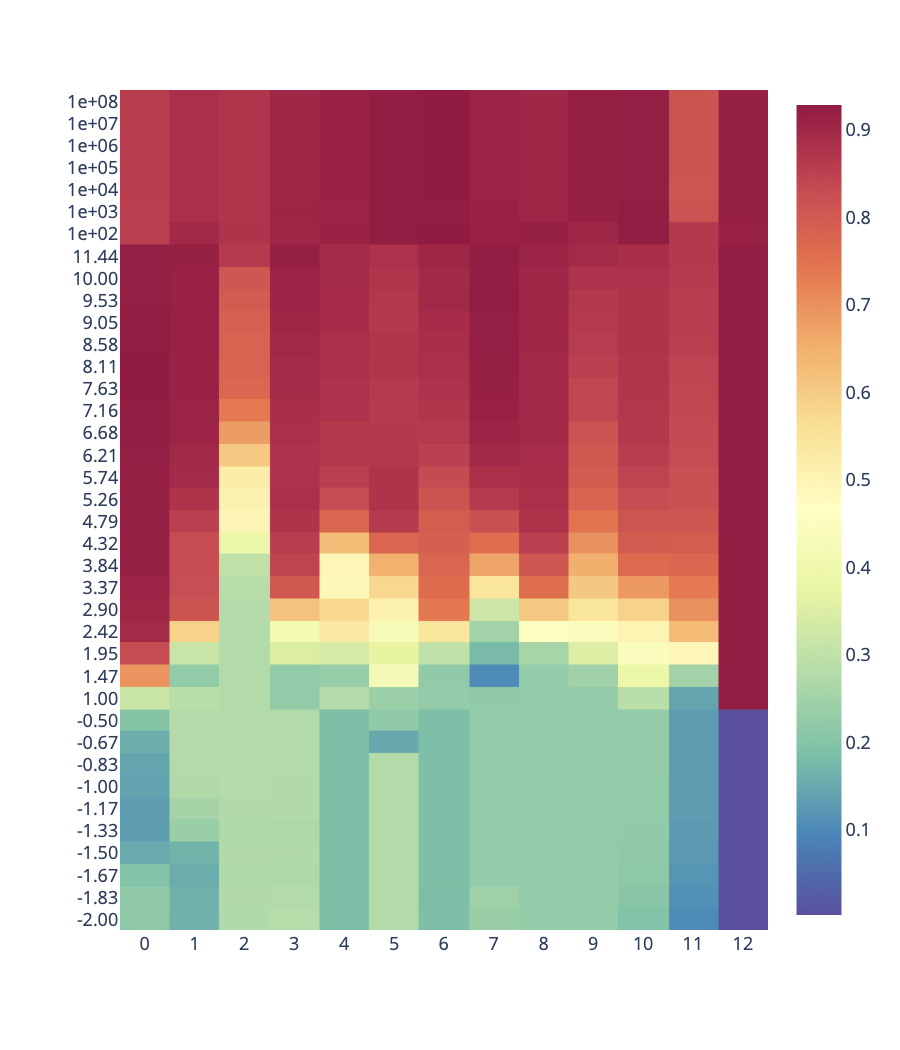
Empirical Validation
We validate scale invariance empirically by training MLPs with different activation functions and rescaling their inputs:
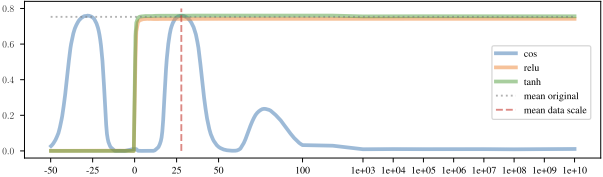
Remarkably, even networks with non-linear activations maintain performance when rescaled near the mean data scale, likely due to the interplay of normalization layers, regularization, and training dynamics.
Well-Behaved Scale Distributions
Analysis of embedding scales across various encoders reveals consistent Gaussian distributions with well-defined means and minimal outliers:
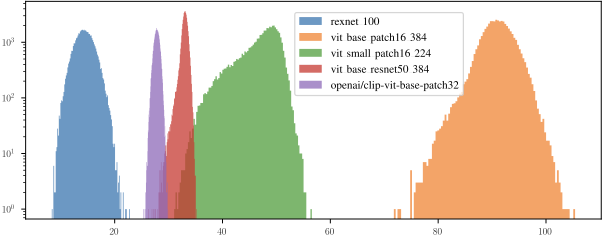
This predictable behavior allows us to confidently rescale decoded embeddings to the target space’s characteristic scale.
Experiments
Intra-Space and Inter-Space Inversion
We first evaluate the quality of our inversion by measuring reconstruction similarity (cosine similarity) between original and reconstructed encodings.
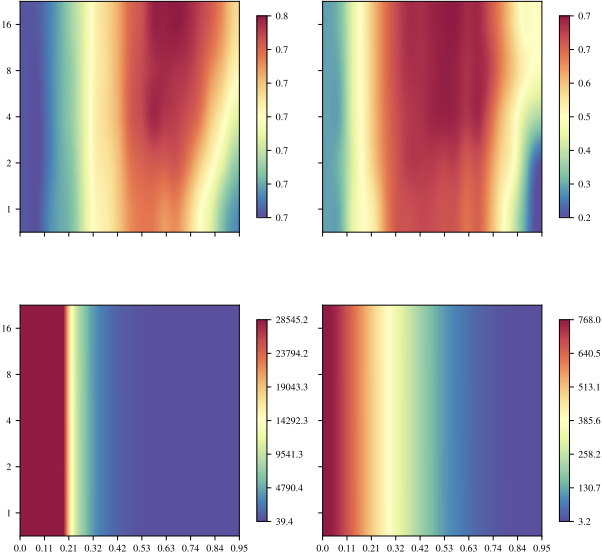
Vision: Using CIFAR-100 and 5 different encoders (3 ViTs, RexNet, CLIP), we test both intra-space inversion (encoding and decoding with the same space’s anchors) and inter-space inversion (across different encoders).
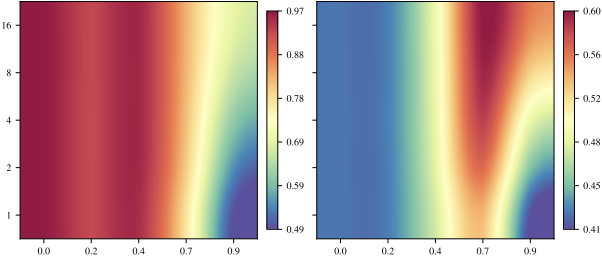
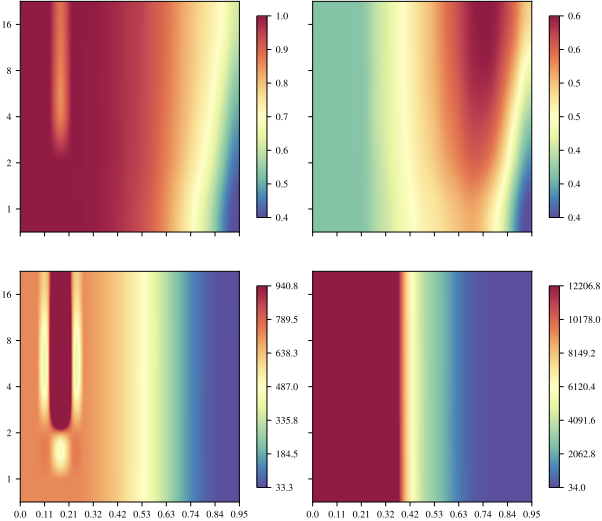
Key findings:
- The inverse achieves medium to high similarity (0.6-0.9), validating the method
- In intra-space settings, $\omega$ (number of subspaces) has minimal impact with low pruning, but compensates for aggressive pruning
- Inter-space translation benefits from the synergy of medium-high pruning with high resampling
Language: Using WikiMatrix parallel multi-lingual data (English, Spanish, French, Japanese) with language-specific RoBERTa encoders, we translate sentences across languages:
| Encoder | Decoder | Absolute | XLM-R | IRP |
|---|---|---|---|---|
| en | en | 1.00 | 1.00 | 0.97 |
| es | en | 0.00 | 0.99 | 0.97 |
| fr | en | -0.02 | 0.99 | 0.97 |
| ja | en | 0.03 | 0.99 | 0.97 |
Our method achieves 0.97 similarity across languages, comparable to the multilingual XLM-R baseline (0.99), while absolute encodings show near-zero similarity without translation.
Zero-Shot Model Stitching
Combining inter-space translation with scale invariance, we demonstrate zero-shot stitching: connecting arbitrary pre-trained encoders with arbitrary pre-trained classifiers.
Experimental Setup: For each dataset, we train classification heads on top of different frozen encoders. We then test all possible (encoder, classifier) combinations using our translation method.
Vision Datasets: MNIST, Fashion-MNIST, CIFAR-10, CIFAR-100 (coarse and fine)
NLP Datasets: TREC, 20 News Groups
| Dataset | ω | δ | Zero-shot | Absolute | Non-stitch | Available |
|---|---|---|---|---|---|---|
| MNIST | 8 | 0.65 | 0.88 ± 0.03 | 0.10 ± 0.03 | 0.97 ± 0.01 | 20 |
| Fashion-MNIST | 8 | 0.65 | 0.82 ± 0.03 | 0.10 ± 0.02 | 0.91 ± 0.01 | 20 |
| CIFAR-10 | 8 | 0.75 | 0.92 ± 0.05 | 0.11 ± 0.04 | 0.95 ± 0.03 | 20 |
| CIFAR-100 (coarse) | 8 | 0.70 | 0.72 ± 0.10 | 0.05 ± 0.01 | 0.88 ± 0.05 | 20 |
| CIFAR-100 (fine) | 8 | 0.75 | 0.62 ± 0.09 | 0.01 ± 0.00 | 0.82 ± 0.07 | 20 |
| TREC | 8 | 0.70 | 0.73 ± 0.09 | 0.22 ± 0.06 | 0.87 ± 0.04 | 20 |
| 20 News | 8 | 0.65 | 0.55 ± 0.10 | 0.05 ± 0.01 | 0.70 ± 0.07 | 20 |
Results show that:
- Absolute (no translation): Near-random performance, limited to same-dimensional spaces (6/20 for vision)
- Zero-shot (IRP): Substantially recovers performance, works across all encoder-decoder pairs (20/20)
- Non-stitch (oracle): Upper bound when encoder and classifier are matched
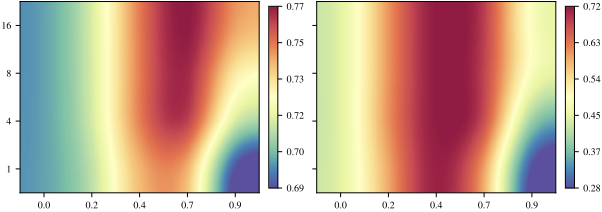
Cross-Domain Stitching
Finally, we test translation between modalities using the 20 News Groups multimodal dataset (text + images).
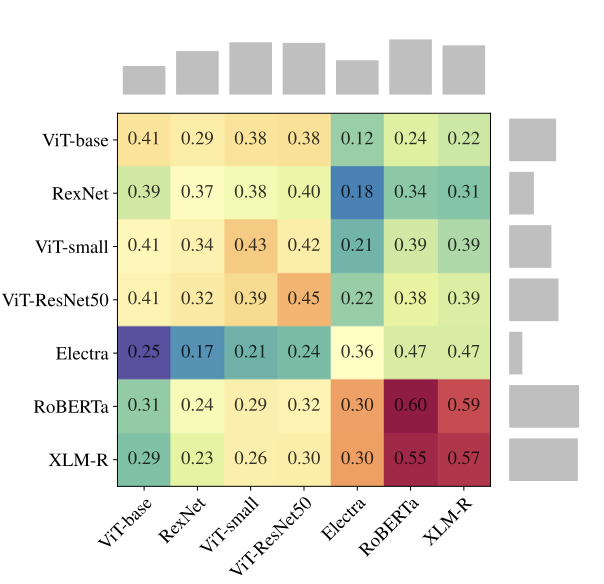
The results demonstrate that IRP successfully translates representations even across vision and language modalities, with language models showing stronger performance as source encoders.
Key Findings
1. Invertibility of Relative Representations
By formalizing the inverse transformation, we can independently map to and from the relative space, enabling true zero-shot compositionality without requiring concurrent access to multiple models.
2. Scale Invariance is Pervasive
Neural classifiers, particularly those with softmax outputs, exhibit remarkable scale invariance properties. Even internal layers maintain performance under rescaling, likely due to the interplay of normalization, regularization, and training dynamics.
3. Stability Through Ensembling
The combination of anchor pruning (selecting orthogonal anchors) and anchor subspaces (ensembling multiple pruned sets) provides a sweet spot between stability and information coverage, with condition number being more important than anchor count.
4. Cross-Domain Translation Works
IRP successfully translates between different modalities (vision and language), demonstrating the generality of semantic alignment in learned representations.
5. Practical Model Reuse
Zero-shot stitching achieves 60-90% of oracle performance across various tasks, making it practical for reusing pre-trained models in new pipelines without any additional training.
Citation
@article{maiorca2024latent,
title = {Latent Space Translation via Inverse Relative Projection},
author = {Maiorca, Valentino and Moschella, Luca and Fumero, Marco and
Locatello, Francesco and Rodol{\`a}, Emanuele},
journal = {arXiv preprint arXiv:2406.15057},
year = {2024}
}
Authors
Valentino Maiorca*1,2 · Luca Moschella*1,2 · Marco Fumero1,2 · Francesco Locatello2 · Emanuele Rodola1
* Equal contribution
1Sapienza University of Rome, Italy · 2Institute of Science and Technology Austria