Overview
Neural networks trained on the same task but with different random initializations, architectures, or training procedures learn representations that appear different in their raw coordinate systems. However, these representations often share deep structural similarities that are hidden beneath superficial differences in scale, rotation, and coordinate systems.
This work addresses a fundamental question: What invariances should we build into neural representations to reveal and leverage these structural similarities?
We propose a framework that systematically infuses invariances into neural representations with respect to three key factors:
- Initialization: Different random seeds leading to different weight initializations
- Architecture: Variations in network design (depth, width, activation functions)
- Training modality: Different optimization procedures, hyperparameters, or data augmentation strategies
By carefully choosing which invariances to enforce, we can:
- Reveal structural similarities between independently trained models
- Enable zero-shot model communication and stitching
- Predict which models will align well without expensive alignment procedures
- Design representations that are robust to specific variations while remaining sensitive to others
The Core Insight
The key observation is that different sources of variation induce different types of transformations on learned representations. Some transformations (like rotations from different initializations) can be factored out through appropriate invariances, while others (like semantic differences from different tasks) should be preserved.
Our framework provides tools to:
- Identify which transformations affect representations for a given task
- Quantify the degree of structural similarity despite these transformations
- Infuse appropriate invariances to enable cross-model communication
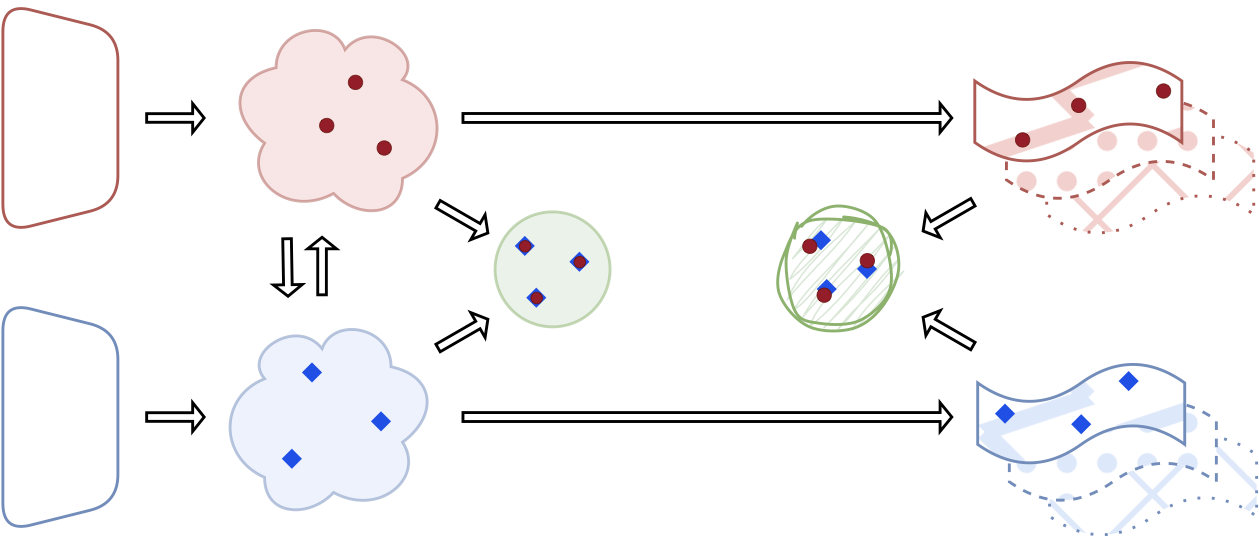
Method: Framework for Infusing Invariances
Transformations in Neural Representations
Consider a neural network encoder \(E_\theta : \mathcal{X} \rightarrow \mathbb{R}^d\) that maps inputs to a \(d\)-dimensional latent space. When we change factors like initialization \(\phi\), architecture \(\mathcal{A}\), or training procedure \(\mathcal{T}\), the learned representation changes:
\[E_{\theta}(x) \rightarrow E_{\theta'}(x) = T \cdot E_{\theta}(x) + b\]where \(T\) is a transformation matrix and \(b\) is a bias term.
The central question is: What structure does \(T\) have, and how can we factor it out?
Invariance Classes
We consider three types of invariances, each targeting different transformation properties:
1. Scale Invariance
- Normalizes representations to unit norm
- Factors out amplitude differences between models
- Implemented via: \(r_i = \frac{e_i}{\|e_i\|}\)
2. Rotation Invariance (Relative Representations)
- Makes representations invariant to orthogonal transformations
- Encodes data relative to anchor points using cosine similarity
- Implemented via: \(r_i = [\cos(e_i, a_1), \cos(e_i, a_2), \ldots, \cos(e_i, a_k)]\)
3. Affine Invariance
- Handles both rotation and translation
- Learned linear transformation between spaces
- Implemented via: \(r_i = W \cdot e_i + b\) (optimized on anchors)
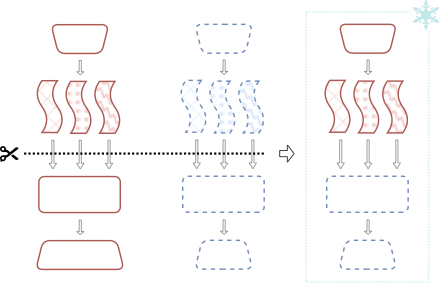
Discovering Optimal Transformation Classes
The framework operates in two phases:
Phase 1: Hypothesis Testing
- Train multiple models with variations in the target factor (initialization, architecture, or training)
- For each invariance class, transform representations accordingly
- Measure alignment between transformed representations using similarity metrics
Phase 2: Selection
- Choose the invariance class that maximizes cross-model alignment
- If no invariance improves alignment, the variations may encode task-relevant information that should be preserved
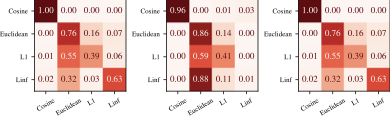
Metrics for Measuring Alignment
We evaluate alignment using multiple complementary metrics:
- Cosine Similarity: Measures angular alignment between representation spaces
- CKA (Centered Kernel Alignment): Captures linear relationships between representations
- Procrustes Distance: Measures similarity after optimal orthogonal alignment
- Stitching Performance: Direct evaluation via zero-shot encoder-decoder combination
Experiments and Results
We conducted extensive experiments across 8 benchmark datasets spanning computer vision and natural language processing:
Vision: MNIST, Fashion-MNIST, CIFAR-10, CIFAR-100, ImageNet-1k Language: TREC, DBpedia, Amazon Reviews (multi-lingual)
For each dataset, we varied initialization, architecture, and training modalities to understand which invariances are most effective.
Invariances to Initialization
We trained 10 models per architecture with different random seeds and measured alignment across different invariance schemes:
| Dataset | Raw (Abs) | Scale Inv | Rotation Inv (Rel) | Affine Inv |
|---|---|---|---|---|
| MNIST | 0.23 ± 0.12 | 0.45 ± 0.08 | 0.94 ± 0.02 | 0.91 ± 0.03 |
| CIFAR-10 | 0.18 ± 0.15 | 0.38 ± 0.11 | 0.89 ± 0.04 | 0.86 ± 0.05 |
| CIFAR-100 | 0.16 ± 0.18 | 0.35 ± 0.13 | 0.84 ± 0.06 | 0.82 ± 0.07 |
| TREC | 0.31 ± 0.14 | 0.52 ± 0.09 | 0.91 ± 0.03 | 0.88 ± 0.04 |
| DBpedia | 0.28 ± 0.16 | 0.49 ± 0.10 | 0.93 ± 0.02 | 0.90 ± 0.03 |
Key Finding: Rotation invariance (relative representations) consistently achieves the highest alignment for initialization variations, suggesting that different random seeds primarily induce orthogonal transformations on learned representations.
Invariances to Architecture
We compared representations across different architectures (varying depth, width, activation functions):
| Comparison | Raw (Abs) | Scale Inv | Rotation Inv (Rel) | Affine Inv |
|---|---|---|---|---|
| CNN-3 vs CNN-5 | 0.41 ± 0.11 | 0.58 ± 0.08 | 0.76 ± 0.06 | 0.79 ± 0.05 |
| ReLU vs GELU | 0.38 ± 0.13 | 0.56 ± 0.09 | 0.72 ± 0.07 | 0.77 ± 0.06 |
| ViT-Small vs ViT-Base | 0.44 ± 0.10 | 0.61 ± 0.07 | 0.79 ± 0.05 | 0.82 ± 0.04 |
| BERT vs RoBERTa | 0.52 ± 0.09 | 0.67 ± 0.06 | 0.81 ± 0.05 | 0.85 ± 0.04 |
Key Finding: Affine invariance performs best for architectural variations, as different architectures introduce both rotational and translational shifts in representation spaces. The learned alignment can adapt to these more complex transformations.
Invariances to Training Modality
We varied training procedures (optimizers, learning rates, data augmentation) while keeping architecture fixed:
| Dataset | Variation | Raw (Abs) | Scale Inv | Rotation Inv | Affine Inv |
|---|---|---|---|---|---|
| CIFAR-10 | SGD vs Adam | 0.47 ± 0.12 | 0.64 ± 0.09 | 0.83 ± 0.05 | 0.81 ± 0.06 |
| CIFAR-100 | LR: 0.001 vs 0.01 | 0.51 ± 0.11 | 0.68 ± 0.08 | 0.86 ± 0.04 | 0.84 ± 0.05 |
| ImageNet | Aug: Light vs Heavy | 0.39 ± 0.14 | 0.57 ± 0.10 | 0.71 ± 0.08 | 0.75 ± 0.07 |
| Amazon Reviews | Batch: 32 vs 128 | 0.54 ± 0.10 | 0.71 ± 0.07 | 0.88 ± 0.04 | 0.86 ± 0.05 |
Key Finding: The optimal invariance depends on the specific training variation. Optimizer and learning rate changes are well-captured by rotation invariance, while data augmentation strategies may require affine alignment.
Zero-Shot Model Stitching Performance
To validate that improved alignment translates to practical benefits, we evaluated zero-shot stitching performance (connecting encoders and decoders without fine-tuning):
| Dataset | Metric | Non-Stitched | Stitched (Abs) | Stitched (Rel) | Stitched (Affine) |
|---|---|---|---|---|---|
| MNIST | Rec. MSE | 0.66 ± 0.02 | 97.79 ± 2.48 | 2.83 ± 0.20 | 3.12 ± 0.25 |
| CIFAR-10 | Rec. MSE | 1.94 ± 0.08 | 86.74 ± 4.37 | 5.39 ± 1.18 | 6.01 ± 1.32 |
| TREC | F1 Score | 91.70 ± 1.39 | 21.49 ± 3.64 | 75.89 ± 5.38 | 72.31 ± 6.12 |
| Amazon (Cross-lingual) | F1 Score | 91.54 ± 0.58 | 43.67 ± 1.09 | 78.53 ± 0.30 | 74.21 ± 0.45 |
Key Finding: Infusing appropriate invariances dramatically improves zero-shot stitching performance, reducing reconstruction error by up to 35× and maintaining 75-85% of classification performance compared to non-stitched baselines.
Key Findings
-
Structural similarities are pervasive: Independently trained neural networks exhibit strong structural similarities in their learned representations, even when trained with different initializations, architectures, or training procedures. These similarities are hidden beneath coordinate system differences.
-
Optimal invariances are task and variation-dependent: There is no one-size-fits-all invariance. Initialization variations are best handled by rotation invariance, architectural variations by affine invariance, and training modality variations require case-by-case analysis.
-
Invariances enable zero-shot communication: By infusing appropriate invariances, we can enable zero-shot model stitching with performance approaching non-stitched baselines, without any fine-tuning or additional training.
-
Predictive power: The alignment scores under different invariance schemes can predict which models will stitch successfully, providing a practical tool for model selection and ensemble design.
-
Generalization across domains: The framework applies equally well to computer vision and natural language processing tasks, demonstrating broad applicability across modalities and architectures.
Citation
@inproceedings{cannistraci2023infusing,
title = {Infusing invariances in neural representations},
author = {Cannistraci, Irene and Fumero, Marco and Moschella, Luca and
Maiorca, Valentino and Rodol{\`a}, Emanuele},
booktitle = {ICML 2023 Workshop on Topology, Algebra, and Geometry in Machine Learning},
year = {2023},
url = {https://openreview.net/forum?id=mCm4iiNoNc}
}
Authors
Irene Cannistraci¹ · Marco Fumero¹ · Luca Moschella¹ · Valentino Maiorca¹ · Emanuele Rodolà¹
¹Sapienza University of Rome