From Bricks to Bridges

Product of Invariances to Enhance Latent Space Communication

ICLR 2024 Spotlight

TL;DR: We construct a product space of multiple relative representations, each computed using different distance metrics (Cosine, Euclidean, L1, L∞), to capture complex transformations between latent spaces without committing to a single invariance a priori. This consistently matches or exceeds the best single metric across vision, text, and graph domains in zero-shot model stitching tasks.

Overview

Neural networks trained under similar inductive biases often learn representations with hidden structural similarities—yet connecting these latent spaces remains challenging. The transformations relating different networks vary unpredictably based on initialization, architecture, dataset, and training dynamics. From Bricks to Bridges introduces a versatile framework that doesn’t require knowing the transformation class a priori.

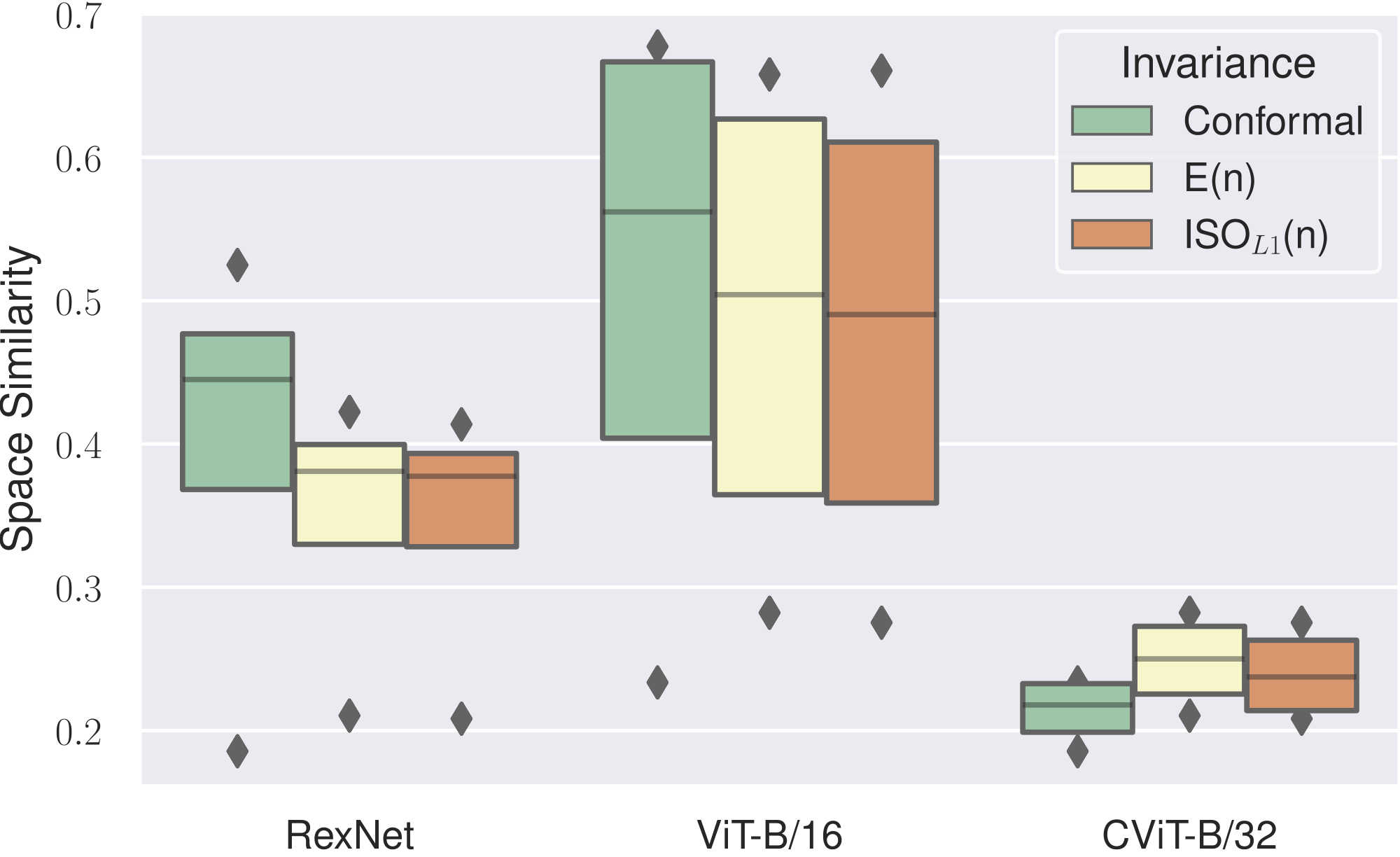
Instead of committing to a single invariance (e.g., angle-preserving transformations), we construct a product space of multiple relative representations, each induced by different distance metrics: Cosine, Euclidean, L1, and L∞. By combining these complementary invariances, we capture complex, nontrivial transformations that enable zero-shot model stitching across architectures, modalities, and training conditions.

Figure 1: Motivation. CKA similarity between pretrained models on Fashion-MNIST measured using different invariances (Conformal, Euclidean, Orthogonal). The diversity in similarity scores highlights the absence of a universal transformation connecting all latent spaces—motivating the need for a product of multiple invariances.

Method: Product of Invariances

The Challenge

When two neural networks learn similar tasks, their latent spaces are related by some transformation T. However, this transformation varies based on:

Random initialization and training dynamics
Architectural differences (CNN vs Transformer, AE vs VAE)
Dataset characteristics (MNIST vs CIFAR vs text vs graphs)
Training objectives (reconstruction vs contrastive learning)

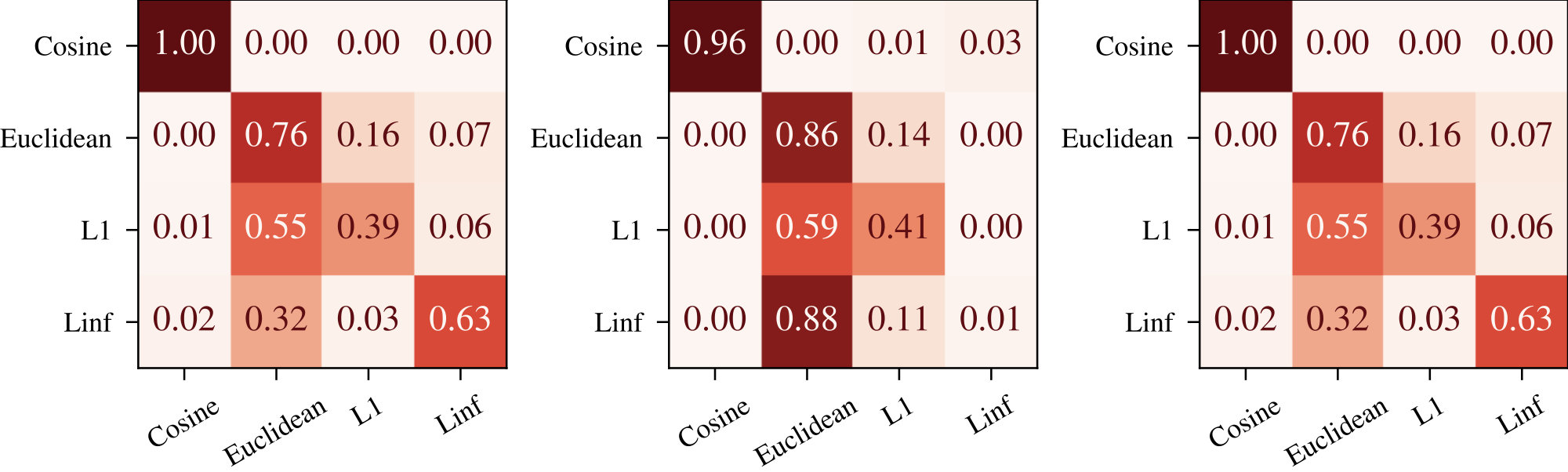
Traditional approaches assume a single metric (typically cosine similarity for angle-preserving transformations) captures this relationship. Our experiments show this assumption fails systematically.

Our Solution: Product Space Framework

We approximate the unknown manifold where representations align by constructing a product space:

\[\tilde{\mathcal{M}} := \prod_{i=1}^N \mathcal{M}_i\]

Each component \(\mathcal{M}_i\) is a relative representation space induced by a different similarity function \(d_i\) (Cosine, Euclidean, L1, L∞), capturing invariances to different transformation classes.

Figure 2: Framework. Given two latent spaces Z and Z' related by an unknown transformation T, we assume there exists a manifold M where samples coincide when projected via π_M. We approximate M by building a product space of relative representations, each computed using a different similarity function invariant to a specific transformation class. The combined representation approximates the true projection.

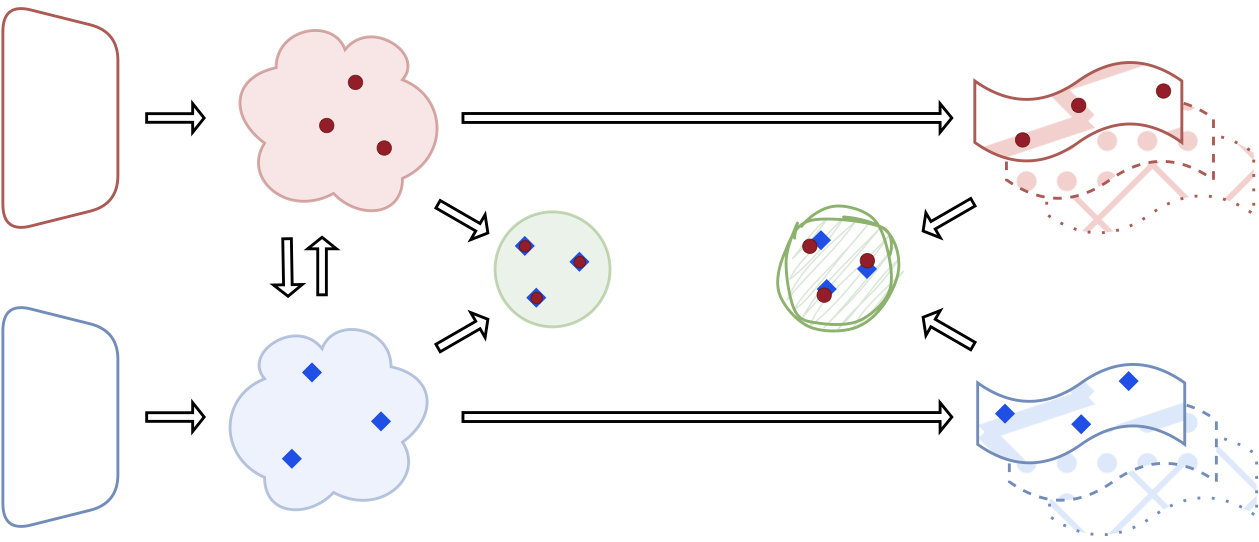
Relative Representations with Multiple Metrics

Given an encoder \(E: \mathcal{X} \to \mathcal{Z}\), anchors \(\mathcal{A} \subset \mathcal{X}\), and similarity function \(d\), the relative representation is:

\[\text{RR}(z; \mathcal{A}, d) = \bigoplus_{a_i \in \mathcal{A}} d(z, E(a_i))\]

We construct four such spaces using:

Cosine: Invariant to angle-preserving transformations (rotations + uniform scaling)
Euclidean: Invariant to orthogonal transformations (rotations + reflections)
L1: Invariant to axis-aligned transformations
L∞: Invariant to coordinate-wise scaling

Aggregation Strategies

We combine these spaces using:

MLP+Sum (Default): Inspired by DeepSets, independently normalize and project each space via MLP (LayerNorm + Linear + Tanh), then sum the results. This maintains constant dimensionality while allowing the model to learn optimal weightings.

Alternatives: Concatenation (increases dimensionality) or Self-Attention (requires fine-tuning for best performance).

Experiments

1. Latent Space Analysis: No Universal Metric

Setup: We analyze cross-seed similarity for models trained from scratch (Autoencoders on MNIST, CIFAR-10/100, Fashion-MNIST) and cross-architecture similarity for pretrained foundation models (5 vision models, 7 text models).

Figure 3: Latent Space Analysis. Left: Cross-seed Pearson correlation for Autoencoders on MNIST shows no single projection consistently achieves highest correlation across architectures. Right: Linear CKA similarity for pretrained models on CIFAR-10 confirms that optimal metrics vary by architecture and dataset.

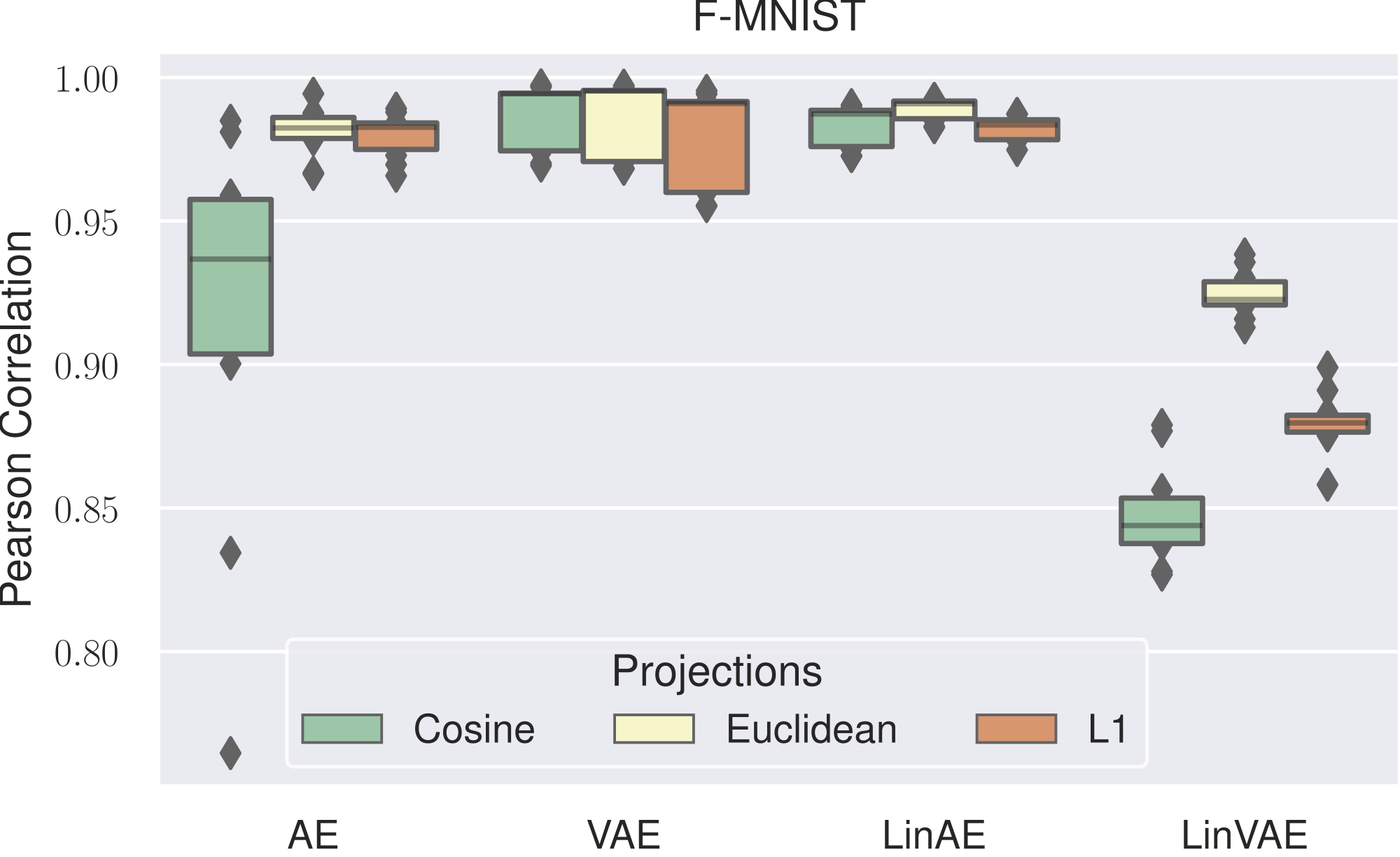
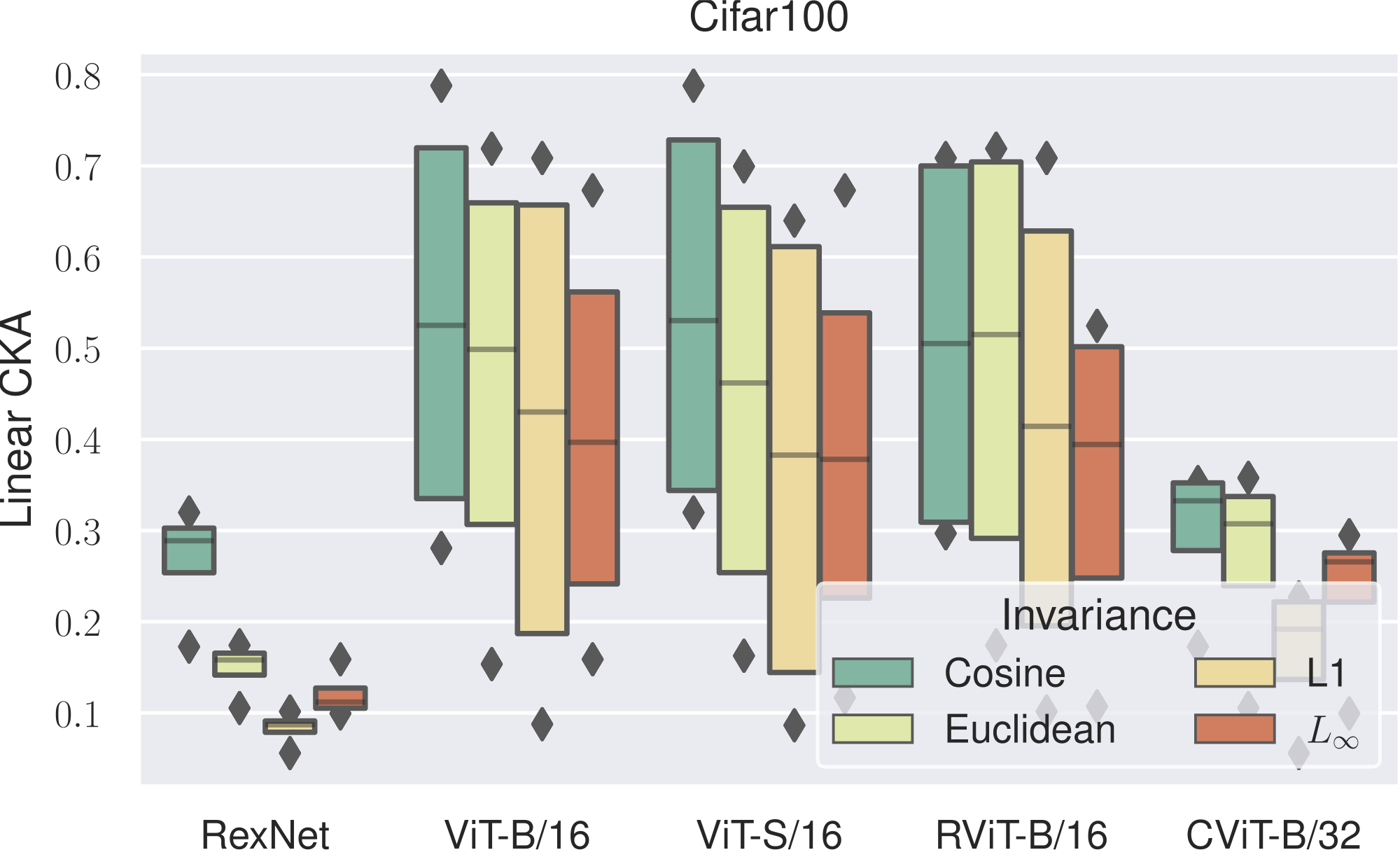
Key Finding: The optimal metric changes systematically based on architecture, dataset, and training conditions. This variability motivates combining multiple metrics rather than choosing one a priori.

2. Zero-Shot Model Stitching

Setup: We perform zero-shot stitching where an encoder from one model is combined with a decoder from another, mediated by our product space representation. No fine-tuning or training occurs—the stitching is entirely zero-shot.

Vision Classification (CIFAR-10/100, MNIST, Fashion-MNIST):

The product of invariances consistently matches or exceeds the best single metric, without prior knowledge of which metric to use.

Encoder	Projection	CIFAR-100	CIFAR-10	MNIST	F-MNIST
CViT-B/32	Cosine	0.52±0.03	0.87±0.02	0.61±0.06	0.68±0.02
	Euclidean	0.53±0.02	0.87±0.02	0.66±0.05	0.70±0.03
	L1	0.53±0.04	0.87±0.02	0.66±0.05	0.70±0.03
	L∞	0.27±0.04	0.52±0.04	0.57±0.03	0.55±0.01
	Product (All 4)	0.58±0.03	0.88±0.02	0.68±0.05	0.70±0.01
RViT-B/16	Cosine	0.79±0.03	0.94±0.01	0.69±0.04	0.76±0.03
	Euclidean	0.79±0.03	0.94±0.01	0.71±0.04	0.77±0.03
	L1	0.77±0.04	0.95±0.01	0.71±0.04	0.79±0.03
	L∞	0.31±0.03	0.75±0.04	0.61±0.05	0.60±0.03
	Product (All 4)	0.81±0.04	0.95±0.01	0.72±0.04	0.76±0.04

Text & Graph Classification:

Modality	Encoder	Projection	DBPedia	TREC	CORA	Stitching Index
Text	ALBERT	Cosine	0.50±0.02	0.54±0.03	-	-
		Euclidean	0.50±0.00	0.60±0.03	-	-
		L1	0.52±0.01	0.65±0.02	-	-
		L∞	0.18±0.02	0.29±0.06	-	-
		Product	0.53±0.01	0.65±0.02	-	-
Graph	GCN	Cosine	-	-	0.53±0.06	0.71
		Euclidean	-	-	0.27±0.06	0.58
		L1	-	-	0.26±0.06	0.58
		L∞	-	-	0.12±0.03	1.00
		Product	-	-	0.77±0.01	1.00

Stitching Index = stitching accuracy / end-to-end accuracy. A value of 1.0 means zero-shot stitching matches end-to-end training.

Remarkable: On CORA graphs, the product space achieves perfect stitching (index 1.0) with 77% accuracy, dramatically outperforming the best single metric (53%).

3. Zero-Shot Image Reconstruction

Setup: Autoencoder image reconstruction on CIFAR-100, stitching encoders and decoders from different training seeds.

Figure 4: Zero-Shot Image Reconstruction. Qualitative reconstruction results on CIFAR-100. Each column shows different encoder-decoder stitching combinations. Rows show results for different projections. The product space (top rows) produces sharp reconstructions comparable to end-to-end models. L∞ alone is blurry, but removing it from the product degrades performance—demonstrating complementarity.

Quantitative Results:

Projection	L1 Error	MSE
Cosine	0.06±0.02	0.20±0.03
Euclidean	0.01±0.00	0.06±0.00
L1	0.01±0.00	0.09±0.00
L∞	0.03±0.01	0.14±0.01
Product (All 4)	0.01±0.00	0.06±0.00
Product (without L∞)	0.02±0.00	0.10±0.01
Absolute (no relative)	0.26±0.06	0.43±0.06

Key Insight: L∞ alone produces blurry images, but removing it from the product space degrades performance. This demonstrates that metrics capture complementary information—even poorly-performing ones contribute crucial details.

4. Ablation: Aggregation Functions

We compare different strategies for combining the four relative spaces:

Aggregation	Vision (RViT-B/16)	Text (BERT-C)	Graph (GCN)
Concat*	0.81±0.00	0.54±0.03	0.75±0.02
MLP+SelfAttention	0.84±0.01	0.51±0.03	0.63±0.13
MLP+Sum	0.85±0.00	0.55±0.04	0.77±0.01
SelfAttention	0.76±0.03	0.36±0.22	0.76±0.02

*Concat increases dimensionality, not directly comparable.

MLP+Sum wins across all modalities: the preprocessing step (normalization + projection) is critical, and simple sum aggregation outperforms complex attention mechanisms in zero-shot settings.

5. Space Selection via Fine-tuning

Setup: Can we learn which spaces are most valuable? We fine-tune only the attention mechanism’s QKV parameters (responsible for blending spaces) on RexNet→ViT-B/16 stitching for CIFAR-100.

Configuration	Accuracy
Cosine (best single metric)	0.50
Product + Zero-shot SelfAttention	0.17
Product + Zero-shot MLP+Sum	0.45
Product + Fine-tuned QKV	0.75
Product + Fine-tuned MLP (classifier)	0.52

Figure 5: Learned Space Selection. Attention weights before and after fine-tuning. Left: Original (uniform). Center: After QKV fine-tuning (shifts to favor Cosine, Euclidean, L1; downweights L∞). Right: After MLP fine-tuning only (unchanged). Fine-tuning space selection is more impactful than fine-tuning the classifier.

Key Finding: Fine-tuning how spaces are weighted (QKV) is more effective than fine-tuning the task-specific classifier. This validates that the product space creates a rich representational substrate where proper “alchemical weighting” of invariances is crucial.

Key Findings

No universal metric exists: The optimal similarity function varies systematically with architecture, dataset, task, and training conditions.
Complementarity is pervasive: Even poorly-performing metrics (L∞) capture information not present in others. Combining metrics consistently outperforms any single choice.
Zero-shot effectiveness: The method enables zero-shot model stitching without training, sometimes achieving perfect stitching indices (1.0 on graphs).
Modality-agnostic: Works across vision (CNNs, ViTs, CLIP), text (BERT family), and graphs (GCNs) with consistent improvements.
Practical robustness: Performance advantage holds across varying hyperparameters (anchor counts, aggregation strategies), making it practical without extensive tuning.
Learnable space selection: When fine-tuning is possible, learning space weightings is more impactful than tuning task-specific layers.

Citation

@inproceedings{cannistraci2024bricks,
  title     = {From Bricks to Bridges: Product of Invariances to Enhance Latent Space Communication},
  author    = {Cannistraci, Irene and Moschella*, Luca and Fumero*, Marco and
               Maiorca, Valentino and Rodol{\`a}, Emanuele},
  booktitle = {International Conference on Learning Representations},
  year      = {2024},
  url       = {https://openreview.net/forum?id=vngVydDWft}
}

Authors

Irene Cannistraci · Luca Moschella* · Marco Fumero* · Valentino Maiorca · Emanuele Rodolà

*Equal Contribution

Sapienza University of Rome, Italy

Related Work: This work extends the Relative Representations framework, which originally used cosine similarity for angle-preserving invariances. By generalizing to multiple metrics and constructing product spaces, we capture complex transformations that single metrics cannot handle.