Bootstrapping Parallel Anchors for Relative Representations

Discovering semantic correspondence between domains with minimal supervision

ICLR 2023 Tiny Papers

TL;DR: We reduce the number of required parallel anchors for relative representations by one order of magnitude through an optimization-based method that discovers new anchors from a minimal seed set. Starting with just 15 seed anchors, our method discovers 300 parallel anchors and often outperforms using ground truth anchors.

Overview

Relative representations enable latent space communication and zero-shot model stitching across different neural networks, but they rely on a critical requirement: parallel anchors—semantically corresponding samples across domains that must be known in advance. In many practical scenarios, obtaining such parallel anchors can be challenging or even impossible.

We present an optimization-based method that discovers new parallel anchors starting from a minimal seed set, reducing the number of required parallel anchors by one order of magnitude. Our approach enables semantic correspondence between different domains, aligns their relative spaces, and achieves competitive results across NLP and Vision tasks.

Background: Relative Representations

Given two domains $\mathcal{X}$ and $\mathcal{Y}$ with embedding functions $E_\mathcal{X}: \mathcal{X} \to \mathbb{R}^n$ and $E_\mathcal{Y}: \mathcal{Y} \to \mathbb{R}^m$, relative representations transform data samples from absolute coordinates to a relative coordinate system defined by a set of anchors $\mathcal{A}_\mathcal{X} \subset \mathcal{X}$ and $\mathcal{A}_\mathcal{Y} \subset \mathcal{Y}$.

For a sample $x \in \mathcal{X}$, the relative representation is:

\[rr(x, \mathcal{A}_\mathcal{X}) = E_\mathcal{X}(x) \mathbf{A}_\mathcal{X}^T\]

where $\mathbf{A}_\mathcal{X}=\bigoplus_{a \in\mathcal{A}_\mathcal{X}} E_\mathcal{X}(a)$ is the row-wise concatenation of anchor embeddings (all normalized to unit norm).

Parallel anchors $\mathcal{A}_p \subseteq \mathcal{A}_\mathcal{X} \times \mathcal{A}_\mathcal{Y}$ are pairs of semantically corresponding anchors that enable cross-domain communication. However, obtaining sufficient parallel anchors is often impractical.

Method: Anchor Optimization (AO)

Our method requires only a small seed set of parallel anchors $\mathcal{L} = \mathcal{L}_\mathcal{X} \times \mathcal{L}_\mathcal{Y} \subseteq \mathcal{A}_p$, where $$

\mathcal{L}

\ll

\mathcal{A}_p

$$. We then optimize to discover the remaining anchors.

Algorithm Overview

The optimization procedure follows these key steps:

Initialize anchor approximation with seed anchors and random embeddings
Compute relative representations for both domains
Estimate correspondence using Sinkhorn algorithm
Optimize anchor embeddings to minimize alignment error
Discretize optimized anchors to actual data samples

Initialization

Without prior knowledge of $\mathcal{A}_\mathcal{Y}$, we initialize:

\[\widetilde{\mathbf{A}}_\mathcal{Y} = \mathbf{A}_{\mathcal{L}_\mathcal{Y}} \oplus \mathbf{N}\]

where $\mathbf{A}_{\mathcal{L}_\mathcal{Y}}$ contains the known seed anchors and $\mathbf{N} \sim \mathcal{N}(0,\mathbf{I})$ are random embeddings for the unknown anchors.

Optimization Objective

We optimize $\widetilde{\mathbf{A}}_\mathcal{Y}$ to align the relative spaces:

\[\argmin_{\substack{\widetilde{\mathbf{A}}_\mathcal{Y} \\ \text{s.t. } ||a||_2=1 \; \forall a \in \widetilde{\mathbf{A}}_\mathcal{Y}}} \sum_{y \in \mathcal{Y}} \text{MSE}(rr(\Pi(y), \mathcal{A}_\mathcal{X}), E_\mathcal{Y}(y) \widetilde{\mathbf{A}}_\mathcal{Y}^T)\]

where $\Pi: \mathcal{Y} \to \mathcal{X}$ is a correspondence estimated at each step using the Sinkhorn algorithm, which exploits the current anchor approximation:

\[\Pi = \text{sinkhorn}_{(x,y) \in \mathcal{X} \times \mathcal{Y}}(rr(x, \mathcal{A}_\mathcal{X}), E_\mathcal{Y}(y) \widetilde{\mathbf{A}}_\mathcal{Y}^T)\]

Discretization

After convergence, $\widetilde{\mathbf{A}}_\mathcal{Y}$ is discretized into $\widetilde{\mathcal{A}}_\mathcal{Y} \subseteq \mathcal{Y}$ by finding the nearest embeddings in $E_\mathcal{Y}(\mathcal{Y})$.

Key Insight: The method iteratively refines anchor positions by leveraging the Sinkhorn algorithm to establish soft correspondences between domains, progressively discovering semantically meaningful anchor pairs from minimal supervision.

Experiments

We evaluate our Anchor Optimization (AO) method across multiple tasks, using only 15 seed anchors to discover 300 parallel anchors. We compare against:

GT (Ground Truth): Using all 300 parallel anchors
Seed: Using only the 15 seed anchors without optimization

Cross-Domain Word Embeddings

We test on two English word embeddings trained on different data: FastText and Word2Vec, with approximately 20K shared vocabulary words.

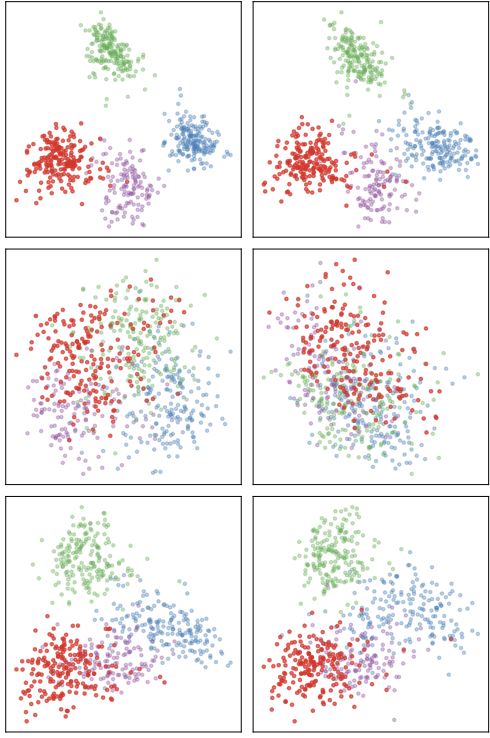
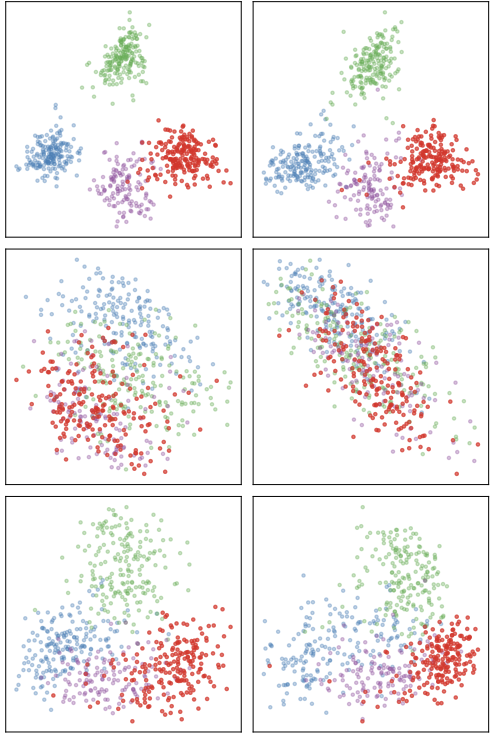
Retrieval Performance Visualization

Optimizing Word2Vec space: Qualitative comparison showing retrieval performance when discovering anchors in the Word2Vec domain. Each row shows results for GT (ground truth), Seed (15 anchors only), and AO (our method). Left column: FastText to Word2Vec. Right column: Word2Vec to FastText.

Optimizing FastText space: Similar results when optimizing the FastText domain instead, demonstrating the method's robustness regardless of which space is being optimized. The method consistently discovers meaningful semantic correspondences.

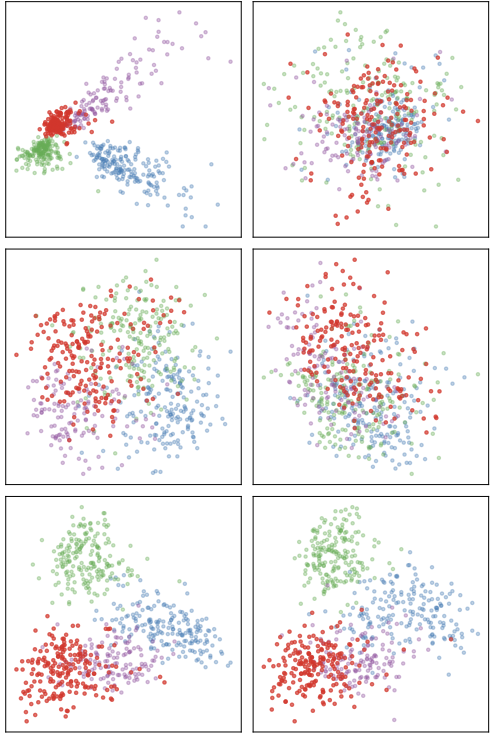
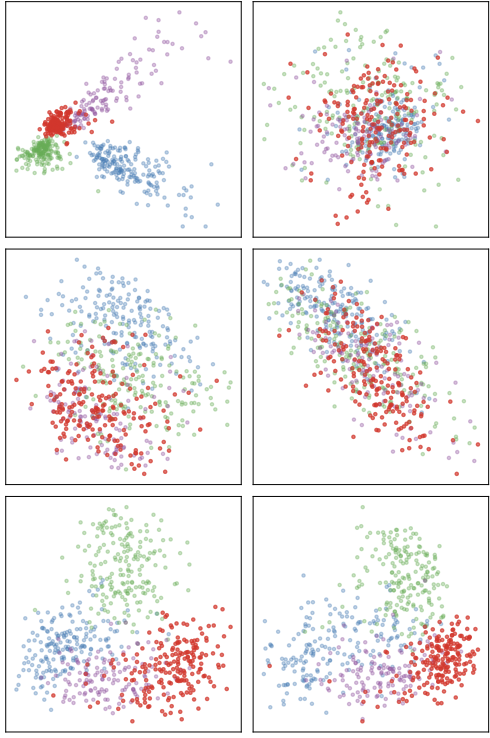
Quantitative Results

Method	Source	Target	Jaccard ↑	MRR ↑	Cosine ↑
GT	FT	W2V	0.34 ± 0.01	0.94 ± 0.00	0.86 ± 0.00
GT	W2V	FT	0.39 ± 0.00	0.98 ± 0.00	0.86 ± 0.00
Seed	FT	W2V	0.06 ± 0.01	0.11 ± 0.01	0.85 ± 0.01
Seed	W2V	FT	0.06 ± 0.01	0.15 ± 0.02	0.85 ± 0.01
AO (Ours)	FT	W2V	0.52 ± 0.00	0.99 ± 0.00	0.94 ± 0.00
AO (Ours)	W2V	FT	0.50 ± 0.01	0.99 ± 0.00	0.94 ± 0.00

Metrics: Jaccard (discrete similarity), MRR (Mean Reciprocal Rank), Cosine (embedding similarity). All metrics computed with K=10 neighbors, averaged over 20K words across 5 random seeds.

Key Result: Our method outperforms even the ground truth in Jaccard index and MRR metrics, demonstrating that the optimized anchors effectively capture semantic correspondence. This surprising result suggests the optimization discovers highly informative anchor positions.

Cross-Lingual Zero-Shot Stitching

We demonstrate cross-lingual model stitching on Amazon reviews in English (en) and Spanish (es), where ground truth parallel anchors are unavailable. Using only 15 out-of-domain (OOD) parallel anchors, our method enables zero-shot stitching: training a classifier on one language and testing on another.

Decoder	Encoder	GT		Seed		AO (Ours)
Decoder	Encoder	F-score ↑	MAE ↓	F-score ↑	MAE ↓	F-score ↑	MAE ↓
en	es	0.51 ± 0.01	0.67 ± 0.02	0.44 ± 0.01	0.80 ± 0.01	0.48 ± 0.01	0.70 ± 0.02
es	en	0.50 ± 0.02	0.72 ± 0.04	0.41 ± 0.01	0.92 ± 0.02	0.46 ± 0.01	0.76 ± 0.02

Zero-shot cross-lingual performance on Amazon Reviews fine-grained classification (5 star ratings). Results averaged over 5 random seeds.

Practical Impact: Our method significantly improves over using seed anchors alone and approaches ground truth performance, enabling practical cross-lingual model stitching in scenarios where extensive parallel supervision is unavailable.

Additional Experiments and Visualizations

Baseline Comparison: Detailed Anchor Space Analysis

To better understand the optimization process, we provide detailed visualizations comparing all three methods (GT, Seed, AO) across both optimization scenarios.

Baseline analysis for Word2Vec optimization: Comprehensive comparison showing the anchor space structure for all three approaches. The visualization reveals how our method (AO) reconstructs semantic structure comparable to ground truth from only 15 seed anchors.

Baseline analysis for FastText optimization: Corresponding baseline visualization when optimizing the FastText domain, demonstrating consistent performance across different optimization targets and embedding spaces.

Understanding the Visualizations

Each visualization shows three rows representing different methods:

GT (Top): Ground truth with all 300 parallel anchors known
Seed (Middle): Using only 15 seed anchors without optimization
AO (Bottom): Our method discovering 285 additional anchors from 15 seeds

The left and right columns show retrieval from FastText to Word2Vec and vice versa, demonstrating bidirectional semantic correspondence.

Vision Domain: Extending to Visual Encoders

Beyond word embeddings, we demonstrate that our method generalizes to the vision domain using different ViT (Vision Transformer) architectures on CIFAR-10.

Cross-Architecture Vision Retrieval

Method	Type	Source	Target	Jaccard ↑	MRR ↑	Cosine ↑
GT	Relative	ViT-base	ViT-small	0.11 ± 0.00	0.27 ± 0.01	0.97 ± 0.00
GT	Relative	ViT-small	ViT-base	0.10 ± 0.00	0.28 ± 0.01	0.97 ± 0.00
Seed	Relative	ViT-base	ViT-small	0.03 ± 0.00	0.03 ± 0.01	0.97 ± 0.00
Seed	Relative	ViT-small	ViT-base	0.03 ± 0.00	0.04 ± 0.01	0.96 ± 0.00
AO (Ours)	Relative	ViT-base	ViT-small	0.10 ± 0.01	0.23 ± 0.03	0.97 ± 0.00
AO (Ours)	Relative	ViT-small	ViT-base	0.10 ± 0.00	0.28 ± 0.01	0.97 ± 0.00

Cross-architecture retrieval on CIFAR-10 using ViT-base (768-dim, pre-trained on JFT-300M + ImageNet) and ViT-small (384-dim, pre-trained on ImageNet). Results demonstrate generalization beyond NLP to vision domains.

Domain Generalization: The method successfully extends to vision tasks, achieving performance comparable to ground truth when bridging different visual encoder architectures with different embedding dimensions and pre-training datasets.

Key Findings

1. Dramatic Supervision Reduction

Our method achieves competitive performance with one order of magnitude fewer parallel anchors (15 vs. 300), drastically reducing annotation requirements.

2. Outperforms Ground Truth

In retrieval tasks, optimized anchors can exceed the performance of using all ground truth anchors, suggesting the optimization discovers highly informative positions.

3. Cross-Domain Effectiveness

Proven effective for both NLP (word embeddings, cross-lingual transfer) and Vision tasks (visual encoders with different architectures).

4. Practical Applicability

Enables latent space communication in scenarios where obtaining extensive parallel supervision is impractical or impossible.

5. No Retraining Required

The method is optimization-based and does not require retraining the underlying models, making it immediately applicable to pre-trained systems.

Citation

@article{cannistraci2023bootstrapping,
  title     = {Bootstrapping Parallel Anchors for Relative Representations},
  author    = {Cannistraci, Irene and Moschella, Luca and Maiorca, Valentino and
               Fumero, Marco and Norelli, Antonio and Rodol{\`a}, Emanuele},
  journal   = {arXiv preprint arXiv:2303.00721},
  year      = {2023}
}

Authors

Irene Cannistraci · Luca Moschella · Valentino Maiorca · Marco Fumero · Antonio Norelli · Emanuele Rodolà

Sapienza University of Rome, Italy

Implementation Details

Optimization Hyperparameters

Optimizer: Adam
Learning Rate: 0.02 (retrieval), 0.05 (stitching)
Optimization Steps: 250 (retrieval), 125 (stitching)
Loss Function: MSE (Mean Squared Error)
Constraint: Unit norm (||a||₂ = 1) via GeoTorch

Sinkhorn Algorithm Settings

Epsilon: 1e-4
Stop Error: 1e-5
Iterations: 1 per optimization step
Purpose: Compute soft correspondence between domains

Tools & Technologies

PyTorch Lightning: Reproducible training pipeline
GeoTorch: Unit norm constraints on anchors
Sinkhorn Algorithm: Fast approximate Wasserstein distances

HuggingFace Transformers: Pre-trained models
HuggingFace Datasets: NLP datasets and CIFAR-10
DVC: Data versioning and experiment tracking

Future Work and Limitations

While this work significantly reduces the number of required parallel anchors, future research directions include:

Eliminating the Seed Requirement

Exploring methods that can discover parallel anchors without any initial supervision through purely unsupervised approaches.

Scaling to Millions of Anchors

Extending the approach to handle very large-scale anchor discovery for applications requiring extensive semantic correspondence.

Multi-Domain Scenarios

Generalizing beyond pairwise domain alignment to multiple domains simultaneously for complex multi-modal systems.